前言

在竞赛当中，解决 LCA 问题有几大方法：倍增，Tarjan，树剖，欧拉序。其中大部分教练推荐的都会是倍增求 LCA 的方法。但在我和 ljt 的讨论下，树链剖分是更加好的求 LCA 的方式。这并不是完全看我们的好恶，首先，倍增是比较容易写挂掉的（尤其是处理直接父亲之类的边界的时候，很容易 RE 或者 WA），而树链剖分只需要进行两次 dfs，即可在$T(n)=O(\log n)$的复杂度下求出 LCA（请注意，这里我用的是算法复杂度上界符号，事实上在实际情况下，链的剖分可能比较少，从而导致复杂度远低于$\log n$，而且树剖的常数更小，详情请见算法复杂度分析一文）；其次，树链剖分更加通用，我们可以利用轻重链剖分解决树上的很多动态问题，甚至拓展一下便是 LCT。所以我就讲一讲树链剖分。

总述

树链剖分，我们使用一下“地理思维”${}^1$顾名思义即可得到是将一棵树剖分成若干根链。

首先，剖分链必须有两条基本规则：1.每个节点在且只在一条链内。2.链上的所有节点两两间都必须是直接相连的。

如下图所示，这是一种树上剖分的方式：

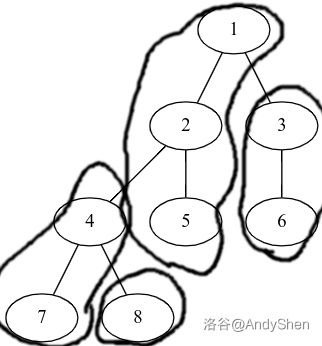
理论上，给出一棵树，我们能够有很多种剖分方式。我们仔细思考一下为什么要树链剖分：树链剖分前，一棵树是有分支的结构，对于每个节点它可能存在若干个不同的后继，此时我们在树上进行操作就会很麻烦，因为这相当于是在一个“二维”的数据结构上面进行操作。而如果树链剖分后，树就被拆分成了一条条链，我们做操作的时候就可以用很多“一维”的方式进行操作，对操作进行了大大简便。

而解决 LCA 问题主要采用的是轻重链剖分，我接下来会讲轻重链剖分的方式及其在 LCA 当中用途。

轻重儿子与轻重链

我们再次运用“拆”字诀，轻儿子是轻的儿子，重儿子是重的儿子。我们怎么来衡量一个点的“轻”和“重”呢？那就是使用这个节点的子节点个数来代表一个节点的轻重，多的就重，少的就轻。例如刚刚那副图，我们如果将每个节点的子节点个数都 dfs 计算出来，然后将每个节点的重儿子都用红色标记出来，就能得到这幅图（红点为重节点，方括号内为子节点个数）：

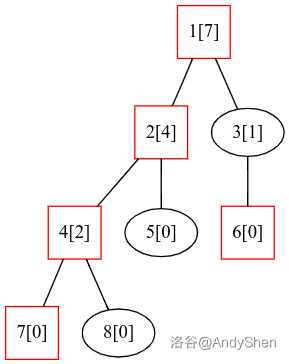
求解重儿子的代码很简单，一次 dfs 即可（为方便理解，我写出所有数组的意义：size 为每个节点的子节点个数；par 为该节点的直接父亲；dep 为该节点深度（在 LCA 当中会用到，但是对于轻重链剖分本身不太重要）；son 为某节点的重儿子编号）：

void dfs1(int x)
{
    size[x] = 1;
    for (auto it : G[x]) {
        if (it == par[x]) {
            continue;
        }
        dep[it] = dep[x] + 1;
        par[it] = x;
        dfs1(it);
        size[x] += size[it];
        if (!son[x] || size[son[x]] < size[it]) {
            son[x] = it;
        }
    }
}

接下来，我们来讲轻重链。如果我们将父节点连接重儿子的边作为重边，连接轻儿子的边作为轻边；那么重边直接相连就得到了重链，对应的轻边直接相连就得到了轻链。那么我们就可以把上面这棵树剖分成下图这个形式：

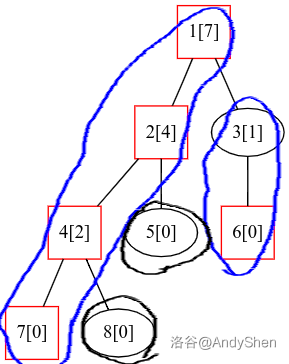
我们怎么样表示轻重链剖分的结果呢？答案是处理出每个节点的链顶，也就是每个节点所在链的深度最小的那个节点。那么很显然，将根作为第一个链顶，对于每个链顶我们将它的所有重儿子（以及重儿子）的链顶置为它，然后对于轻儿子递归，将轻儿子作为新的链顶，继续进行操作（可以自行对着前面这幅图操作一番）代码如下（top 数组记录链顶）：

int top[MAX_N];
void dfs2(int x, int tx)
{
    top[x] = tx;
    if (son[x]) {
        dfs2(son[x], tx);
    }
    for (auto it : G[x]) {
        if (it == par[x] || it == son[x]) {
            continue;
        }
        dfs2(it, it);
    }
}

从树链剖分到 LCA

在开始将树链剖分的 LCA 之前，我们先讲一讲传统的 LCA。传统的 LCA 是这样：深的那个节点往上跳跳到和浅的那个节点深度相同，判断一下他们有没有跳到同一位置，如果没有，那么一起往上跳到同一位置为止，代码如下：

int lca(int u, int v)
{
    while (dep[u] > dep[v])
        u = parent[u];
    while (dep[v] > dep[u])
        v = parent[v];

    while (u != v) {
        u = parent[u];
        v = parent[v];
    }
    return u;
}

我们仔细回想回想，这个算法慢在哪里：慢在每次只能一步步跳，不能够快速的“飞”到某个位置。

为了这个问题，倍增 lca 用的是维护 2 的幂次方父亲的方式，然后快速跳转快速判断。那么树链剖分类似的，我们是跳到链顶。

我们将这个问题倒退回去考虑：对于节点$u$和$v$，如果$u=v$，那么显然的，$u$和$v$的 lca 就是它们。然后倒退一步：如果$u$和$v$在一条链上，也就是链顶相同，那么也很显然的，$u$和$v$的 lca 是它们当中深度较浅的那一个。OK，接下来我们对于任意节点$u$和$v$，考虑其链顶的深度，将链顶深度较深的那个节点跳转到链顶的父亲，如此循环往复，直至其链顶相同为止，此时就符合前面的那种情况，输出深度较浅的那个就行了。

int lca(int u, int v)
{
    while (top[u] != top[v]) {
        if (dep[top[u]] > dep[top[v]]) {
            u = par[top[u]];
        } else {
            v = par[top[v]];
        }
    }
    return dep[u] > dep[v] ? v : u;
}

然后我给出P3379（LCA 板子题）的树剖解决方案：

#include <bits/stdc++.h>

using namespace std;

constexpr int MAX_N = 500010;
vector<int> G[MAX_N];
#define DEBUG 0

int size[MAX_N], dep[MAX_N], son[MAX_N], par[MAX_N];

void dfs1(int x)
{
    size[x] = 1;
    for (auto it : G[x]) {
        if (it == par[x]) {
            continue;
        }
        dep[it] = dep[x] + 1;
        par[it] = x;
        dfs1(it);
        size[x] += size[it];
        if (!son[x] || size[son[x]] < size[it]) {
            son[x] = it;
        }
    }
}

int top[MAX_N];
void dfs2(int x, int tx)
{
    top[x] = tx;
    if (son[x]) {
        dfs2(son[x], tx);
    }
    for (auto it : G[x]) {
        if (it == par[x] || it == son[x]) {
            continue;
        }
        dfs2(it, it);
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int n, m, s;
    cin >> n >> m >> s;
    int u, v;
    for (int i = 1; i <= n; i++) {
        G[i].reserve(20);
    }
    for (int i = 1; i <= n - 1; i++) {
        cin >> u >> v;
        G[u].emplace_back(v);
        G[v].emplace_back(u);
    }
    dep[s] = 1;
    par[s] = -1;
    dfs1(s);
    dfs2(s, s);
    int a, b;
    for (int i = 1; i <= m; i++) {
        cin >> a >> b;
        while (top[a] != top[b]) {
            if (dep[top[a]] >= dep[top[b]]) {
                a = par[top[a]];
            } else {
                b = par[top[b]];
            }
        }
        cout << (dep[a] < dep[b] ? a : b) << endl;
    }
#if DEBUG
    for (int i = 1; i <= n; i++) {
        printf("%d:size:%d;depth:%d\n", i, size[i], depth[i]);
    }
#endif
    return 0;
}

后记

树剖解决 LCA 问题，一方面在于树剖事实上比较好调试，因为它的几个步骤并没有很强的耦合，我可以一个个拆开来调试，也比较容易发现问题。而倍增 LCA 不具有这个性质。

LCA 问题，是图论当中一个很重要的问题，在算法竞赛中有很多种考法，一种是类似仓鼠找 Sugar之类的利用 LCA 去做判断的题目，此类题最难不过蓝题，如果要再难就得是用数学知识了，比如仓鼠找 Sugar II；一种是类似ZJOI2012 灾难一样的题，这个题只能使用倍增，因为要在树上进行动态维护（当然，树剖也能办，就是 ljt 说的 LCT 解决，我毛估估可以，但没考证过），然后从这个题也可以继续延伸出去到Lengauer-Tarjan 算法，这里我就不赘述了。

解决 LCA 问题除了大多数树上说的倍增（离线更新，离线查询），此处我讲的树剖（离线更新，在线查询）以及延伸的 LCT（在线更新，在线查询），欧拉序（不了解），然后我再给出一个 Tarjan 算法（静态更新，离线查询）的代码，自行参考学习：

#include <bits/stdc++.h>

using namespace std;

constexpr int N = 500010;
vector<int> query[N];
vector<int> T[N];
vector<pair<int, int>> tasks;
unordered_map<int, unordered_map<int, int>> ans;

// Union Find Set
int par[N];
int findpar(int n)
{
    return par[n] == n ? n : par[n] = findpar(par[n]);
}
void unite(int a, int b)
{
    a = findpar(a);
    b = findpar(b);
    par[b] = a;
}

// Tarjan's LCA Algorithm
bool vis[N];
void tarjan(int n, int far)
{
    for (auto it : T[n]) {
        if (it == far) {
            continue;
        }
        tarjan(it, n);
    }
    vis[n] = true;
    for (auto it : query[n]) {
        if (vis[it]) {
            ans[n][it] = findpar(it);
            ans[it][n] = ans[n][it];
        }
    }
    unite(far, n);
}

int main()
{
    cin.tie(nullptr);
    cout.tie(nullptr);
    ios::sync_with_stdio(false);
    // freopen("data/p3379.in", "r", stdin);
    int n, m, s;
    cin >> n >> m >> s;
    for (int i = 1; i <= n; i++) {
        par[i] = i;
    }
    int x, y;
    for (int i = 1; i <= n - 1; i++) {
        cin >> x >> y;
        T[x].push_back(y);
        T[y].push_back(x);
    }
    for (int i = 1; i <= m; i++) {
        cin >> x >> y;
        tasks.emplace_back(x, y);
        query[x].push_back(y);
        query[y].push_back(x);
    }
    tarjan(s, s);
    for (auto it : tasks) {
        cout << ans[it.first][it.second] << endl;
    }
    return 0;
}

只要有关系的地方，就存在图。LCA 算法作为一个经典算法，应该被一代又一代 OI 人探究出新的考察方式，探索出新的内容。

Notes and References

[1]：我们的班主任上地理课的时候经常和我们强调地理思维，关键在于两个字：“拆”和“猜”。此处使用的便是“拆”字诀。这两条是遇到新名词时理解的一个常用手段。