图论:求解支配树：Lengauer-Tarjan算法

Andy Shen2023/4/20大约 13 分钟

前言

在编译器开发的优化当中，Lengauer-Tarjan 算法作为求解支配树的高效算法被广泛使用。该算法也在 NOI 大纲的 NOI 级内容当中，而且能够解决一些倍增 LCA 的题（如 ZJOI2012 灾难）。此处就大概介绍一下这个算法。

本文将分为如下几个部分：术语，算法证明，算法内容，Notes（注释），Reference（引用），后记。

以下内容主要来自 Thomas Lengauer 和 Robert Endre Tarjan 的论文以及虎书（现代编译原理），一部分是直接翻译，有的我加上了一些个人理解。以下内容如果来自参考文献的会加上对应的无方括号的角标。有的地方我会给出注释放在 Notes 当中，右上角会加上带有方括号的角标。

术语和符号

生成树(spanning tree) 定义 $^{3}$ ：一个无向图的生成树是这个无向图的无环子图。通常我们得到一颗生成树会通过 dfs 的方式，每次 dfs 经过的合法路径（到达未访问节点的路径）全部联通就是生成树。

支配点(dominator) 定义 $^{1}$ ：当一点 $v$ 支配另外一点 $w$ 时，从根 $r$ 到 $w$ 的任意一条路径必定经过 $v$ 。

直接支配点(immediate dominator, also $i d o m$ ) 定义 $^{1}$ ：当 $v$ 支配 $w$ 且 $w$ 的其他支配点支配 $v$ 时，此时 $v$ 是 $w$ 的直接支配点。（通俗的讲，就是距离该节点最近的支配点）

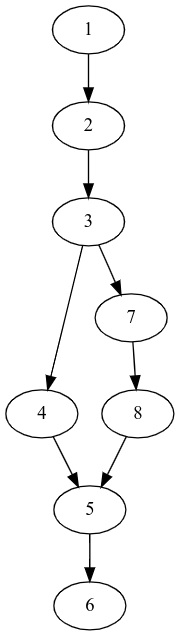
半必经节点(semidominator, also $s d o m$ ) 定义 $^{2}$ $^{[1]}$ ：在生成树中，如果 $n$ 的某一祖先 $s$ 出现分叉边，且在 $n$ 处又重新汇合，那么 $n$ 的半必经节点就是 $s$ ，如果不存在这种情况，那么它的父亲当中 dfn 值最小的就是它的半必经节点。

如下图所示，节点编号是它的 dfs 序，5 的祖先节点 3 出现分叉边，而该分叉边又在 5 处汇合，故 5 的半必经节点就是 3；而 2 的祖先节点到 1 并没有分叉边，那么 2 的半必经节点就是 1。

支配树(dominator tree) 定义 $^{1}$ ：所有由 $(i d o m (w), w)$ 作为边所组成的树就是支配树，其符合一个性质：当 $v$ 支配 $w$ 时， $v$ 在支配树当中必为 $w$ 的祖先。

$x \rarr^{*} y$ 定义： $x$ 在生成树中为 $y$ 的祖先

$x \rarr^{+} y$ 定义： $x \rarr^{*} y a n d x \neq y$

算法证明 $^{[2]}$

接下来是关于 Tarjan 算法的证明部分，由于通过证明过程可以更好的理解算法，所以我将它放在算法部分的前面。如果你对此不感兴趣，可以直接跳到下一节。

定理 1

内容

对于流图（带根图） $G = (V, E, r)$ 中，任一非根节点只有唯一直接支配点。支配树（定义见前文）符合一个性质：当 $v$ 支配 $w$ 时， $v$ 在支配树当中必为 $w$ 的祖先。

证明 $^{[3]}$

首先我们将这个问题拆成两半：问题一：唯一直接支配点；问题二：支配树的性质

对于问题一，我们考虑使用反证法：

假设某一节点 $w$ ，存在两个不同支配点 $u, v$ （事实上，对于多个点也类似的），那么按照直接支配点定义，可以得到 $u$ 支配 $w$ ， $v$ 支配 $w$ ，且 $u$ 支配 $v$ ， $v$ 支配 $u$ ，根据支配的定义，不存在这样的 $u$ ， $v$ （支配点不是自己，支配点支配别人还支配自己怎么可能）。所以该命题不成立。从而说明 $w$ 只有唯一的直接支配点。

对于问题二，根据性质是很容易得到的，此处不再赘述。

引理 1

内容

对于图中两节点 $v$ ， $w$ ，如果 $v \leq w$ $^{[4]}$ ，那么任意 $v$ 到 $w$ 的路径必定经过它们在生成树当中的 lca。

证明 $^{[5]}$

如果 $v$ 是 $w$ 的某一祖先，则 $v$ 到 $w$ 路径必过它们的 lca $v$ ，问题成立。

否则， $v$ 和 $w$ 在不同子树上，那么 $v$ 到 $w$ 路径必定经过 lca。

引理 2

内容

对于任意 $w \neq r$ ， $i d o m (w) \rarr^{+} w$ 。

引理 3

内容

对于任意 $w \neq r$ ， $s d o m (w) \rarr^{+} w$ 。

令 $p a r (w)$ 为 $w$ 的父亲，通过半必经节点的定义（见前文）我们可以知道 $s d o m (w) \leq p a r (w) < w$ ，且存在一条路径 $s d o m (w)$ ~ $w$ ，这个路径中间的所有节点 $v_{i}$ （不包含起点终点）都应该满足 $v_{i} > w$ 。根据引理 1 我们可以知道， $s d o m (w)$ ~ $w$ 的路径上一定存在它们的 $l c a$ ，这个 $l c a$ 应该满足 $l c a \leq s d o m (w)$ 。我们组合一下前面的不等式可以得到 $l c a \leq s d o m (w) \leq p a r (w) < w < v_{i}$ ，如果 $v_{i}$ 当中包含了 $l c a$ ，会得到 $l c a < l c a$ 的结论，这个结论是荒谬的，所以它们的 $l c a$ 一定是 $s d o m (w)$ 和 $w$ 中一点，由于 $s d o m (w)$ 的 $d f n$ 更小，所以 $s d o m (w)$ 必定是 $w$ 的祖先，即 $s d o m (w) \rarr^{+} w$

引理 4

内容

对于 $w \neq r$ ， $i d o m (w) \rarr^{+} s d o m (w)$ 。

证明

根据引理 2、3 可以得到 $i d o m (w)$ 和 $s d o m (w)$ 都是 $w$ 的祖先。我们将从 $r$ 到 $w$ 的路径分成两部分：一部分是 $r$ ~ $s d o m (w)$ ，另一部分是 $s d o m (w)$ 到 $w$ 。如果 $i d o m (w)$ 在后一部分当中，根据半必经节点的定义我们会得到 $w$ 和 $s d o m (w)$ 之间不止一条路径，此时 $i d o m (w)$ 不能支配 $w$ ，和 $i d o m (w)$ 的定义是不符合的，所以 $i d o m (w)$ 一定在前一部分当中。既然在前一部分，那么显然 $i d o m (w) \rarr^{+} s d o m (w)$ ，原命题成立。

引理 5

内容

对于 $v$ ， $w$ 满足 $v \rarr^{*} w$ ，有 $v \rarr^{*} i d o m (w)$ 或者 $i d o m (w) \rarr^{*} i d o m (v)$ 。

证明 $^{[6]}$

令 $x$ 为 $i d o m (v)$ 的任一子代，且 $x$ 为 $v$ 的祖先。根据定理 1 和直接支配点定义，一定存在一条 $r$ 到 $v$ 的路径可以避开 $x$ （如果避不开，那么 $x$ 也是个必经节点，且这个点离 $v$ 更近，也是 $v$ 的直接支配点。但是根据直接支配点的唯一性可以知道这不成立，所以一定能避开）。我们将 $v$ 到 $w$ 的路径接到 $r$ 到 $v$ 后面，可以得到 $r$ 到 $w$ 避开 $x$ 的一条路径。所以如果 $i d o m (w)$ 在 $i d o m (v)$ 和 $v$ 之间的话，从 $r$ 到 $w$ 就不一定需要经过 $i d o m (w)$ ，这和直接必经节点的定义相悖。所以 $i d o m (w)$ 必须是 $v$ 的后代或者是 $i d o m (v)$ 的祖先。

通过以上五个引理和定理 1，我们可以得到接下来几个重要的定理。（事实上，这些结论是在支配树问题当中十分常用的结论，在 Harel 的线性支配树求解的论文当中有几个引理就和这里一样的）

定理 2

内容

对于 $w \neq r$ ，假设任意符合 $s d o m (w) \rarr^{+} u \rarr^{*} w$ 的 $u$ 满足 $s d o m (u) \geq s d o m (w)$ ，那么 $i d o m (w) = s d o m (w)$ 。

证明

考虑任意一条路径 $p$ 从 $r$ 到 $w$ ，令 $x$ 是这个路径 $p$ 上符合 $x < s d o m (w)$ 的最后的一个 $x$ （最近的一个 $x$ ）。如果不存在这样的 $x$ ，那么说明 $s d o m (w) = r$ 显然是支配 $w$ 的。对于其它情况，令 $y$ 是满足 $s d o m (w) \rarr^{*} y \rarr^{*} w$ 在 $x$ 后的第一个节点（离 $x$ 最近的那个符合条件的点，也应该是距离 $s d o m (w)$ 最近的那个节点）。令路径 $q$ 是从 $x$ 到 $y$ 的路径，显然 $q$ 是 $p$ 的一部分。接下来我们使用反证法证明这条路径不考虑两端的所有点都大于 $y$ 。假设存在一些路径 $q$ 上面的节点 $v_{i}$ 满足 $v_{i} < y$ 。根据引理 1，肯定存在对应的 $v_{j}$ 满足 $i \leq j \leq k - 1$ 是 $y$ 的祖先。由于我们对 $x$ 的选择，以及 $v_{j} \geq s d o m (w)$ ，我们可以得到 $s d o m (w) \rarr^{*} v_{j} \rarr^{*} y \rarr^{*} w$ ，这和我们对 $y$ 的选择相悖，从而说明这条路径不考虑两端的所有点都大于 $y$ 。（此处我简单解释一下，由于 $x$ 是 $s d o m (w)$ 前面的那个节点，所以路径中间的节点一定是 $s d o m (w)$ 自己或者后代，从而得到 $s d o m (w) \rarr^{*} v_{j}$ ，又由于我们根据引理 1 得到的结论， $v_{j} \rarr^{*} y$ ，组合一下就得到 $s d o m (w) \rarr^{*} v_{j} \rarr^{*} y \rarr^{*} w$ 。但是由于 $y$ 是 $s d o m (w)$ 后面的第一个节点，不应该存在 $v_{j}$ 距离 $s d o m (w)$ 更近，此处就会出现悖论。）

然后我们将这几个结论合并一下。首先，我们证明了 $x$ 到 $y$ 路径中间所有节点都大于 $y$ ，又 $s d o m (w)$ 在 $x, y$ 之间，那么就可以得到 $s d o m (w) > y$ 。根据半必经节点的定义，我们有 $y > s d o m (y)$ 。再考虑对 $x$ 的选取，我们可以得到 $x < s d o m (w)$ 。由于 $x$ 可能和 $s d o m (y)$ 是同一个节点，所以我们将这些不等式组合起来就可以得到 $s d o m (y) \leq x < s d o m (w)$ 。但是根据命题的假设当 $s d o m (w) \rarr^{+} y \rarr^{*} w$ 时有 $s d o m (y) \geq s d o m (w)$ ，这和前面的那个不等式相悖，说明 $s d o m (w) \neq y$ 不成立，即 $s d o m (w) = y$ 且 $s d o m (w)$ 在路径 $p$ 上。由于这个路径的选择是任意的，所以 $s d o m (w)$ 支配 $w$ ，即得 $i d o m (w) = s d o m (w)$ 。

定理 3

内容

令 $w \neq r$ ，取 $u$ 为满足 $s d o m (w) \rarr^{+} u \rarr^{*} w$ 中 $s d o m (u)$ 最小的点。然后对于 $s d o m (u) \leq s d o m (w)$ 满足 $i d o m (u) = i d o m (w)$

证明

结论 1（必经节点定理）

内容

对于非根节点 $w$ 且 $u$ 是满足 $s d o m (w) \rarr^{+} u \rarr^{*} w$ 当中 $s d o m$ 值最小的，那么有：

i d o m (w) = {\begin{aligned} s d o m (w) & i f s d o m (w) = s d o m (u) \\ i d o m (u) & o t h e r w i s e \end{aligned}

证明

定理 2 和定理 3 的直接结论。

定理 4（半必经节点定理）

前面的定理都讲的是如何从半必经节点推证出必经节点，此处讲如何计算半必经节点。

内容

对于任一节点 $w \neq r$ ，存在

s d o m (w) = m i n (v | (v, w) \in E a n d v < w \cup s d o m (u) | u > w a n d t h e r e i s a n e d g e (v, w) s u c h t h a t u \rarr^{*} v

证明

让 $x$ 等于

算法内容

标准做法

标准做法极其简单无脑，我们先删掉一个节点 $v$ ，然后 dfs 一遍，跑一下还能跑到那些节点，把还能跑到的节点的集合记作 $S$ ，那么原来的点集 $V$ ,排除掉这个被删掉的节点本身，再排除掉剩下能够跑到的节点，那么就是这个节点 $v$ 的支配点。写成数学形式就是 $A n s = V - v - S$ 。算法复杂度 $O (m n)$ （依次删除每个节点复杂度 $n$ ，dfs 一次 $m$ ）。

Aho-Ullman 算法 $^{4}$ $^{[7]}$

Aho 和 Ullman 采用的做法也不是很复杂，它先弄了一个长度为 $n$ 的 bitset，然后我们对每个节点使用二进制进行一个编码，最后遍历全图然后使用位运算等方式搞出支配点。对于 bitset 的操作，复杂度是 $O (n)$ ，然后对于每个节点每条边，复杂度是 $O (m n)$ ，所以总复杂度是 $O (n^{2} m)$

Lengauer-Tarjan 算法

Harel 算法

In fact，求解支配树当然还有更快的方法，也就是 Harel 算法，该算法的复杂度是 $O (n)$ ，此处限于个人能力暂时就先不写了，有需求的可以上ACM Digital Library上自行查阅。

Notes

[1]: Lengauer 和 Tarjan 论文里面对半必经节点的定义是 $s d o m (w) = min {v | there is a path v = v_{0}, v_{1}, . . ., v_{k} = w such that v_{i} > w for 1 \leq i \leq k - 1}$ ，简单的讲，就是对于从某一点 $v_{0}$ 出发到 $w$ 的路径，这条路径符合中间的所有节点的 dfn 值（起点终点不算）都大于 $w$ ，取这条路径上的 dfn 最小值便是 $s d o m (w)$ （此时的路径要算上起点终点）。观察一下很显然的，只有旁叉路径才会出现其 dfn 值都大于 $w$ ，所以这个表述和虎书当中的表述在本质上是相同的。而虎书上的表述更加容易明白一点（因为虎书的表述有 tarjan 缩点算法的韵味）。但是虎书当中的表述有一点小瑕疵，那就是当不存在分叉节点的时候就会不知道其半必经节点是谁，此处对于这种情况的表述是我根据 Lengauer 和 Tarjan 的论文加上去的。

[2]: 此处的内容如果不加特别说明则代表来自 Lengauer 和 Tarjan 的论文（Reference 1），此后不再赘述。加了括号的内容基本上是为了促进理解而加的注释。

[3]: 该证明在 Lengauer 和 Tarjan 论文里面并没有证明（或许说，是直接引到了两篇参考文献上去），此处的证明是我根据虎书上面的证明结合自行理解得到的。

[4]: 这里的比大小比的是 dfs 后它们的 dfn 序的大小，为了简洁起见以及尊重原论文的写法，此处就直接进行比大小，下面类似的不再赘述。

[5]: 该证明在 Lengauer 和 Tarjan 论文当中并无给出，比较简单我按照自己想法写了一下。

[6]: Lengauer 和 Tarjan 论文当中在证明 $r$ 到 $v$ 路径有多条时的原文是By Theorem 1 and Corollary 1，但是我分析了一下上下文逻辑，引理 5 用结论 1 和定理 1 证明，结论 1 用定理 2 和定理 3 证明，定理 3 用引理 5 证明。这里会出现循环论证，个人觉得这里是不对的，事实上证明这个结论也用不到Corollary 1，我按照我自己的理解写了。

[7]: Aho 和 Ullman 的算法我大概就提个思路，这不是本文的主要目的，有兴趣可以自己去探讨。

Reference

1.Thomas Lengauer and Robert Endre Tarjan. A Fast Algorithm for Finding Dominators
in a Flowgraph. ACM Transactions on Programming Languages and Systems, Vol. 1, No. 1, July 1979, Pages 121-141.(原文可以看 ACM Digital Library，该文没有中文版，自行翻译)

2.Andrew W. Appel and Maria Ginsburg. Modern Compiler Implementation in C，Pages 443-450（现代编译原理（C 语言描述），人民邮电出版社，赵克佳、黄春、沈志宇译，第 310-315 页），此书后面都简称为“虎书”

3.OI Wiki 上面对生成树的定义

4.Aho, A.V.,And Ullman,J.D. Principles of Compiler Design. Addison Wesley, Reading, Mass., 1977.