图论基础1:概念与术语

Andy Shen2022/12/20大约 13 分钟

引言

生活中我们会遇到很多问题：比如张三和李四认识但是和王五不一定认识；滨和路到龙翔桥可以直接通地铁，但滨和路到萧山国际机场却要换乘。这些问题似乎都有些共性：如果我们把人，地铁站这些对象看成点；把人际关系，地铁线路看成边，从而将这些点连起来，我们可以通过这一幅图中观察出一些性质。其中，这个图形就叫做图（Graph），研究这个性质的理论就叫做图论（Graph Theory）。

图的定义

严格的讲，图 $G$ 的一般数学定义是一个三元组 $(V, E, ϕ)$ ，其中 $V$ 和 $E$ 是两个不相交的集合， $V$ 非空， $ϕ$ 是 $E$ 到 $V$ 的一个映射， $V$ 、 $E$ 、 $ϕ$ 分别被称为图 $G$ 的顶点集、边集、关联函数 $^{[1]}$ 。当然，这样表示过于复杂，我们往往会使用一个二元组 $(V, E)$ 来表示一个图，将关联函数融入边集中（关联函数这种表达方式此处不讲，到讲有限自动机的时候会再讲讲这个东西）。

一般的，点集里面我们会使用数字来代表这个节点，这个数字就叫做节点编号，点集合 $V = {1, 2, 3, 4, \dots, n}$ 。边我们通常会用一个二元组 $(u, v)$ 来表示（此处 $u, v$ 都是节点编号）。有向图中 $(u, v)$ 代表的是节点 $u$ 指向节点 $v$ 的一条边，也可以表示成 $u \rarr v$ ；无向图中 $(u, v)$ 代表的是节点 $u$ 和节点 $v$ 之间的一条边。（这两个东西的定义下面讲）

图的术语

图当中有很多术语，我一一解释：

以下的示例都指的是无边权的图。

有向图和有向边：

我举个例子，蛤四有个巨佬叫做 ljt，我初中的时候听说过他，但是他初中的时候不知道我，此时我和他之间是单向的关系，那么如果我们都是一个节点，我们两个之间的边就是单向边，如果一幅图中所有的边都是单向边，那么这幅图就叫做有向图(directed graph)。

显然的，有向图中的边对应的二元组 $e = (u, v)$ 是有序的（意思就是不能调换成 $(v, u)$ ），此时的这个边 $e$ 就叫做有向边(directed edge)（在不引起混淆的情况下可以叫做边(edge)），也可以称为弧(arc)（这种叫法在网络流当中比较常见）,此时 $u$ 被称作 $e$ 的起点(tail)， $v$ 被称作 $e$ 的终点(head)（为什么起点叫做 tail?你仔细看看这个箭头 $\rarr$ ，左边的这个叫尾巴，右边的这个叫头，所以箭头是从起点指向终点，也是从尾巴指向头），这两个点都叫做 $e$ 的端点(endpoint)， $u$ 是 $v$ 的直接前驱， $v$ 是 $u$ 的直接后继。

无向图和无向边 $^{[2]}$ ：

无向图很好理解，比如我和一个人是朋友，那么我是她的朋友，她也是我的朋友，我们这是互相的关系，此处的边对应的二元组 $e = (u, v)$ 就是无序的（可以调换成 $(v, u)$ ，其中 $u, v \in V$ ），这个边就叫做无向边(undirected edge)，简称边(edge)，这两个点就叫做端点(endpoint)

在竞赛当中，我们经常会把无向图当成双向有向图看待，就是对于无向图当中的每一个边都建成两条端点相同，方向相反的边从而处理。（它们的结果是相同的，比如 $a$ 认识 $b$ ， $b$ 认识 $a$ ，那么和 $a, b$ 互相认识是一个意思，只是在定义的时候，他们不一样）

有限图和无限图

学过集合的应该知道，集合可以是有限的集合，叫有限集，也可以是无限的集合，叫无限集。如果一个图当中的点集和边集都是无限集，那么这个图就叫做无限图；如果点集和边集都是有限集，那么这个图就叫做有限图（不要问我为什么不存在点集无限，边集无限或者反过来的情况，这种情况是毫无意义的，因为你很难弄出跳转关系）

我们通常说的图一般是有限图。

入度和出度

度(degree) 在有向图和无向图当中意义不太一样，在有向图当中分两种，一种叫入度(in-degree)，一种叫出度(out-degree),简单的讲，入度就是指向这个节点的边的数目，或者说，是到这个节点终止的边的数目；出度就是从这个点出发的边的数目。在无向图当中，度指的就是和这个节点相连的边的数目。

入边和出边

和前面入度与出度类似的，对于一个节点来说，入边就是指向它的边；出边就是从它出发的边。

带权值图和权值边

有的图当中这个边是带有权值的，比如从滨和路到龙翔桥坐地铁要 4 块钱，那么滨和路到龙翔桥的这条边就要一个 4 的权值，这个时候我们应该怎么办呢？很简单，只要拓展一下边的定义即可。原来我们对于边的定义是一个二元组 $e = (u, v)$ ，我们现在给它加一个元表示权值，那么这个边就变成了 $e = (u, v, c)$ ，此处的 $c$ 就是权值。

一般地，我们的图表示的时候可以带上权值，也可以不带权值，这两种情况代码小有差异，但总体思路不变。

孤点，重边，自环

这三个概念比较显然，我一起讲了。

无向图中，孤点指的是一个没有任何边与它连接的点；重边指的是两点之间存在多条边（这些边的权值可以不同）；自环指的是自己与自己之间有一条边。

有向图中大体类似，孤点指的是没有任何入边或者出边的点；重边指的是节点 $u$ 到节点 $v$ 存在多条方向相同的边（权值可以不同）；自环指的是自己有一条指向自己的边。

图的存储

图的存储用很多种方法，按照 OI Wiki 上的说法，有存边，邻接矩阵，邻接表，链式前向星四种做法。从个人观点以及参考书上的说法看 $^{[4]}$ ，存边的做法只在 Kruskal 算法当中会用到，到那个地方再说；链式前向星才算的上真正意义上的邻接表；而 OI Wiki 上的所谓邻接表，味道有点不正，你说它是优化的邻接矩阵也可以，你说它是邻接表好像也没什么问题，所以单独拎出来讲。

下面的示例代码，我将实现这几个功能（函数）：添加一条边，查询两个点之间是否有边（并输出权值），以及深搜整张图输出经过节点编号（每个节点只经过一次）。

邻接矩阵

为了表示图，我们引入了一个东西，叫做矩阵。什么叫做矩阵？矩形的数字阵叫做矩阵。如下所示，一个矩阵分成若干行和若干列。

[\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix}]

那么怎么用它来表示图呢？假设第 $i$ 行第 $j$ 列有一个数字 $c$ ，那么我们就将它等价成前文说的用来表示边的三元组 $e = (i, j, c)$ ，意思就是点 $i$ 到点 $j$ 有一条边，边权是 $c$ 。但是呢这样有个小问题，如果点 $i$ 到点 $j$ 并不存在一条边怎么办呢？很简单，将它填充成一个表示没有边的特殊数字即可（一般会是 0，因为长度为 0 的边不怎么常见，而全局数组默认都是 0；如果真的遇到长度为 0 的边，那么填充成 0x3f,-1(0xff)都有，只要你自己不会混淆且数据范围不会干扰到就行）

这个矩阵一定是 $n$ 行 $n$ 列的,所以这个矩阵又称方阵（正方形的数阵）

在无向图中，正如前文所说，我们会将其建成有向图，其中每个边都有两个方向，你可以自己拿一下纸笔画一下一个无向图对应的矩阵，显然是对称的。

接下来我们看一个示例加深一下理解：

对于如下的矩阵：

[\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 9 & 8 & 10 & 0 & 0 & 0 \\ 0 & 0 & 0 & 10 & 0 & 5 & 0 \\ 0 & 0 & 0 & 6 & 8 & 10 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 8 \\ 0 & 0 & 4 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

这说明了：

从 1 出发没有任何节点

从 2 出发指向了 2，3，4；边权分别是 9，8，10。

从 3 出发指向了 4，6；边权分别是 10，5。

从 4 出发指向了 4，5，6；边权分别是 6，8，10

从 5 出发指向了 7；边权是 8

从 6 出发指向了 3；边权是 4

从 7 出发没有任何节点

画出来的图是这样的：

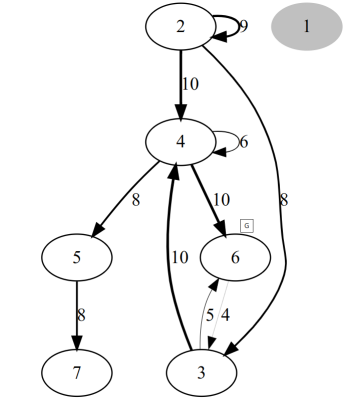
代码：

constexpr int MAX_N = 100;
int G[MAX_N][MAX_N];
int n, m; //节点数，边数

void addEdge(int u, int v, int c)
{
    G[u][v] = c;
    //如果是无向图的话要加一句G[v][u] = c;
}

int hasEdge(int u, int v)
{
    return G[u][v];
}

bool vis[MAX_N];

void dfs(int u)
{
    if (vis[u]) {
        return;
    }
    vis[u] = true;
    cout << u << ' ';
    for (int i = 1; i <= n; i++) {
        if (G[u][i] != 0) {
            dfs(i);
        }
    }
}

常见操作复杂度 $^{[3]}$

操作	复杂度
需要空间	$V^{2}$
添加一条边	$O (1)$
查询两点是否相连	$O (1)$

优势

实现简单，速度快

劣势

占用空间大，无法处理重边，遍历的时候会做大量的无效操作（就是在没有边的地方要一直空判）

vector 优化的邻接矩阵（也可以认为是邻接表）

在邻接矩阵当中，我们发现了很多问题，其中最大的问题就是无法处理重边以及大量空间的浪费。

让我们想一想，在邻接矩阵当中什么导致了空间浪费？是大量的“0”。假如我们把边看成萝卜，那么邻接矩阵的做法就是先挖足够的坑，然后将所有的边一个萝卜一个坑填进去。这会导致两个问题：1、有很多空的坑。2、我没法一个坑放好几个萝卜，而我也不能够新挖坑（处理重边的时候遇到的就是这个问题）。

如何优化，这就涉及到 STL 里面一个东西叫做 vector 了，vector 相比传统的数组，它支持一个操作，那就是向后插入元素。这对解决我们的问题就很有用了，相当于我能够做到来一个萝卜挖一个坑，既不会有多出来的坑，遇到重边的时候我可以给它再挖一个坑，而不用和原来的坑之间“打架”。

我们为了实现这个目的，我们会声明一个 vector 指针数组，第一维代表了索引，就是从这个编号代表的点出发的边的一个 vector，然后 vector 里面储存终点编号和边权。从而达到这个效果。

代码：

typedef pair<int, int> P;
constexpr int MAX_N = 100;
vector<P> G[MAX_N];
int n, m; //节点数，边数

void addEdge(int u, int v, int c)
{
    G[u].emplace_back(v, c);
    //如果是无向图的话要加一句G[v].emplace_back(v,c);
}

int hasEdge(int u, int v)
{
    for (auto it : G[u]) {
        if (it.first == v) {
            return it.second;
        }
    }
    return 0;
}

bool vis[MAX_N];

void dfs(int u)
{
    if (vis[u]) {
        return;
    }
    vis[u] = true;
    cout << u << ' ';
    for (auto it : G[u]) {
        dfs(it.first);
    }
}

常见操作复杂度(degree(V)代表的是一个点的度，按照大 O 标记法的定义，可以看成 O(V))

操作	复杂度
需要空间	$E + V$
添加一条边	$O (1)$
查询两点是否相连	$d e g r e e (V)$

我们来模拟一下链式前向星的插入过程：

1、读入起点u，终点v，边权c，声明一条新的边edges[k]并附好值

2、edges[k]的nxt置为head[u]，head[u]置为k(就是现在的开头指向原来的开头，然后开头更新为现在的开头)

以前面邻接矩阵的那个图为例，我们画出来就是这样：

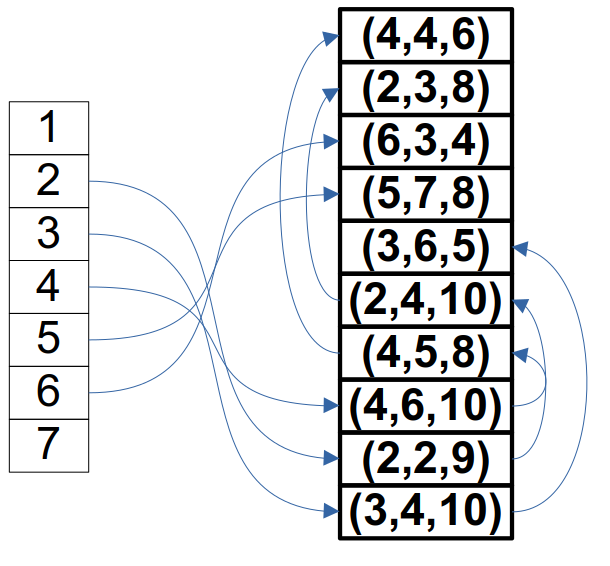
代码：

constexpr int MAX_N = 100; //最多点数
constexpr int MAX_M = 1000; //最多边数
int head[MAX_N];
struct Edge {
    int v, c, nxt; //默认下一个是-1（因为下标不可能是-1，而且用-1在遍历的时候有好处）
} edges[MAX_M];
int cnt; //用来标记下一个声明到哪里了
int n, m; //节点数，边数

void init()
{
    for (auto& edge : edges) { //因为我要修改原值，所以这个地方要用引用
        edge.nxt = -1;
    }
    for (int& i : head) {
        i = -1;
    }
    cnt = 0;
}

void addEdge(int u, int v, int c)
{
    edges[cnt] = { v, c, head[u] };
    head[u] = cnt;
    cnt++;
}

int hasEdge(int u, int v)
{
    //如果遍历到末尾，那么它的下一个是-1,-1对应的是0xff，按位取反后就是0，也就是false
    for (int i = head[u]; ~i; i = edges[i].nxt) {
        if (edges[i].v == v) {
            return edges[i].c;
        }
    }
    return 0;
}

bool vis[MAX_N];

void dfs(int u)
{
    if (vis[u]) {
        return;
    }
    vis[u] = true;
    cout << u << ' ';
    for (int i = head[u]; ~i; i = edges[i].nxt) {
        dfs(edges[i].v);
    }
}

常见操作复杂度(之所以说 vector 法是邻接表，因为它复杂度什么的和这个一样)

操作	复杂度
需要空间	$E + V$
添加一条边	$O (1)$
查询两点是否相连	$d e g r e e (V)$

优势

占用空间极小，可以处理重边，遍历较为简单，在网络流中处理反边比较容易,在老一辈 OIer 以及网络流当中常用。

劣势

查询两点速度慢，实现和理解比较复杂。

References

[1]:数学奥林匹克小丛书（高中卷）17：图论 P1

[2]:这几节基本来自OI Wiki，在部分难懂的地方我加了解释

[3]:这里指的都是最大复杂度，复杂度的表示请详见算法复杂度分析一文

[4]:《算法（第四版）》，英文原著为"Algorithms(Fourth Edition)"，Robert Sedgewick, Kevin Wayne 著，谢路云译，人民邮电出版社出版