字符串处理(下)
拓展 KMP 算法(Z Algorithm)*
拓展(ex-ten-sion):范围或操作的扩大。
——韦氏词典
拓展 KMP,又称 Z 函数,他解决了这样一个问题:"abacaba"时,它的
这个问题朴素的做法显然是
vector<int> z_function_trivial(string s) {
int n = (int)s.length();
vector<int> z(n);
for (int i = 1; i < n; ++i)
while (i + z[i] < n && s[z[i]] == s[i + z[i]]) ++z[i];
return z;
}正如它名字当中有 KMP 一样,它的复杂度可以低到
实际上,拓展 KMP 的思路和 Manacher 比较像:维护一个最大区间,当位置超界时暴力更新。
接下来,我们定义匹配段Z-Box为区间
接下来,我们不断维护右端点尽可能大的匹配段
,也就是
,如图: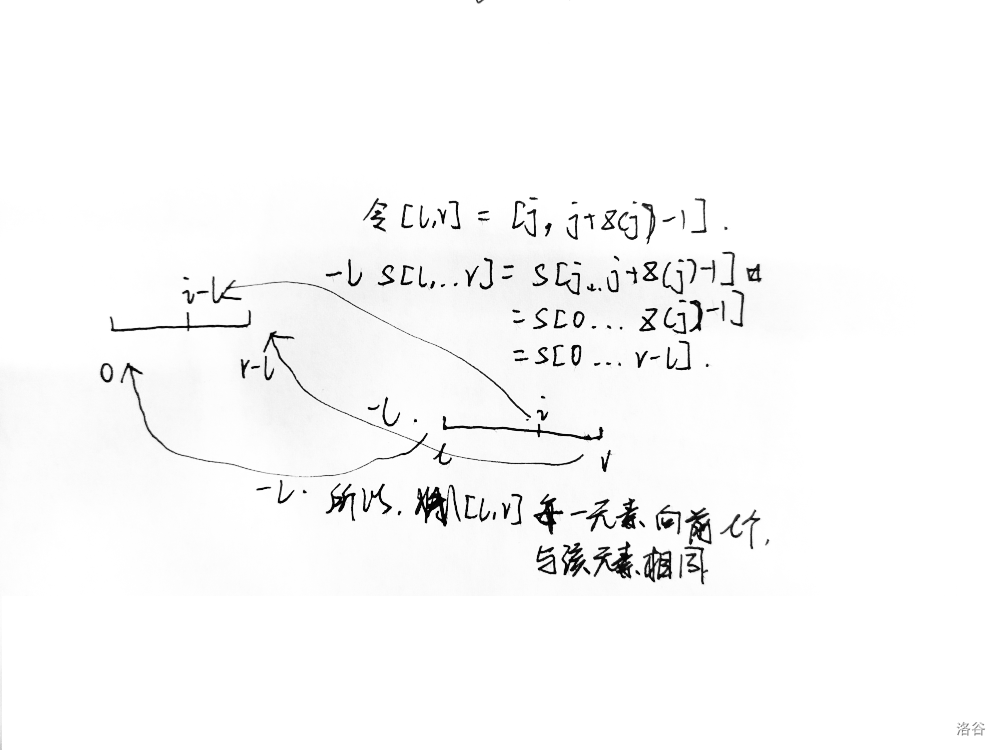
所以如果当
那么如果
最后,根据
vector<int> z_function(string s) {
int n = (int)s.length();
vector<int> z(n);
for (int i = 1, l = 0, r = 0; i < n; ++i) {
if (i <= r && z[i - l] < r - i + 1) {
z[i] = z[i - l];
} else {
z[i] = max(0, r - i + 1);
while (i + z[i] < n && s[z[i]] == s[i + z[i]]) ++z[i];
}
if (i + z[i] - 1 > r) l = i, r = i + z[i] - 1;
}
return z;
}应用
例一 匹配串
既然叫拓展 KMP,肯定能解决 KMP 的问题。在这里,我们将模式串pat放在src后面,并且中间用#隔开,接下来我们求解pat的长度,说明此时的前缀已经完全出现了一次pat,所以就可以解决 KMP 问题。
Aho-Corasick Automaton*.
结合(com-bine):使成为一体。
——韦氏词典
AC 自动机,又称 Aho-Corasick Automaton。(记住,不是自动 AC 机,这里的 AC 不是 Accepted,这个自动机是 Automaton 而不是 Automation,学完这个东西既不能保证你能 AC 所有的题目也不能保证你这个自动机写的对。)用一句话讲就是:在 Trie 上跑 KMP。
首先,我们要讲一下 AC 自动机的用途:就是 KMP 的拓展版,与 KMP 相比,AC 自动机有多个模式串,一个原串,然后统计模式串在原串当中的出现。
接下来我们详细介绍 AC 自动机的构建以及使用。
首先,AC 自动机是基于 Trie 的,所以当你读入字符串的时候应该将它构建成一棵 Trie。接下来,我们要考虑一个东西叫做失配指针
我们来类比一下 KMP 和 AC 自动机的思路:KMP 当字符失配的时候,我们将利用已经匹配的内容,计算出匹配部分的前缀后缀最大相同长度,然后将模式串的这个前缀移动到与后缀对齐。类似的,AC 自动机的失配指针就是指向与当前节点所代表的字符串的后缀在字典树上对应的节点(当然,这个节点必须存在),如下图所示:
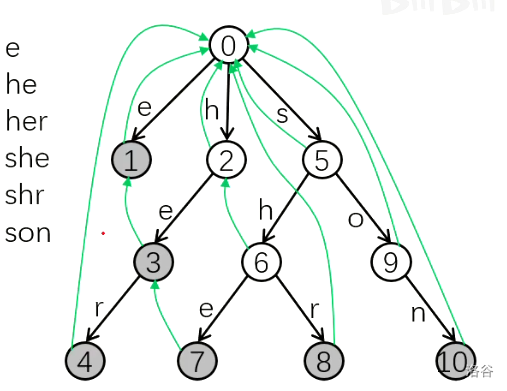
仔细观察 6,7 两个节点,他们所代表的字符串
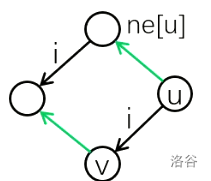
这四个点组成了一个平行四边形,所以我们将这个法则叫做“平行四边形法则”。
这样子就完了吗?还不够,我们考虑这样一种情况:两个模式串分别是"abc","bcd",原串是"abcd",这两个串在不同的子树上,但是我希望统计完"abc"后继续统计"bcd"。这就是我们要考虑的第二个法则:三角形法则。当统计完"abc"后,此时在一个叶子节点上,由于"bc"后缀又在字典树当中出现过了,所以我们可以利用这一部分已经匹配的内容,那么,我们就为这个叶子结点建转移边到它的回退边的对应儿子上,就是如下图所示:
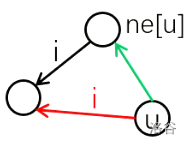
这一条叫做三角形法则。
好,AC 自动机构建完成了,那么我们怎么统计呢?我们在原串上进行对应跳转,然后自动机上沿着转移边跳转,然后我们再用一个指针沿着回退边去统计答案,然后输出即可。
Code
#include <bits/stdc++.h>
using namespace std;
constexpr int MAX_N = 1000010;
int nxt[MAX_N], trie[MAX_N][26], cnt[MAX_N], alloc;
void insert(const string& str)
{
int cur = 0;
for (auto it : str) {
if (trie[cur][it - 'a'] == 0) {
trie[cur][it - 'a'] = ++alloc;
}
cur = trie[cur][it - 'a'];
}
cnt[cur]++;
}
void build()
{
queue<int> Q;
for (auto it : trie[0]) {
if (it != 0) {
Q.push(it);
}
}
while (!Q.empty()) {
int u = Q.front();
Q.pop();
for (int i = 0; i < 26; i++) {
int v = trie[u][i];
if (v != 0) {
nxt[v] = trie[nxt[u]][i];
Q.push(v);
} else {
trie[u][i] = trie[nxt[u]][i];
}
}
}
}
int query(const string& str)
{
int ans = 0;
int cur = 0;
for (auto it : str) {
cur = trie[cur][it - 'a'];
for (int j = cur; j && ~cnt[j]; j = nxt[j]) {
ans += cnt[j];
cnt[j] = -1;
}
}
return ans;
}
int main()
{
// freopen("data/P3808_2.in", "r", stdin);
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
string ts;
cin >> ts;
insert(ts);
}
build();
string t;
cin >> t;
cout << query(t) << endl;
return 0;
}习题
后缀数组*
后缀(suf-fix):出现在单词末尾的词缀。
——韦氏词典
待补。
后缀 trie 与后缀树*
压缩(com-presss):减小尺寸、数量或体积。
——韦氏词典
首先我们来讲讲后缀 Trie,后缀 Trie 一句话就能讲完:将一个字符串的全部后缀都插入到前缀树(字典树)中。举个例子,我们将字符串"abbb"的全部后缀插入一个前缀树,就应该是这样的:
这棵后缀 Trie 有什么用呢?首先我要说:它存储了所有子串的信息,所以,他可以用来解决很多子串的问题。为什么这么说呢?你可以观察一下,一棵后缀树从根出发到叶子节点所组成的字符串,恰好是原串的子串。这绝非巧合:我们取后缀,相当于给一个串提供了一个左边界;而我们使用字典树的路径,就相当于取了后缀的前缀,就是给这个串一个右边界。这样子组成的新串,当然是原串的子串了。
但是这样就够了吗?你会发现,为了构建一棵后缀 Trie,你会消耗大量的空间,因为你要把每个后缀都加入进去。而对这个东西的压缩,就有两种方案:后缀树和后缀自动机。
后缀树的压缩思路比较暴力:如果一个节点的儿子不是叶子结点,且它只有一个儿子,那么就将它和儿子合并。
Suffix Automaton*
构造(con-struct):通过组合或排列零件或元素来制作或形成。
——韦氏词典
我们仔细观察刚刚到后缀树会发现,如果我们把这棵树变成一个 DAG,那么这个图当中有大量节点是不必要的,也就是我们可以把这棵树表达的信息压缩成如下图所示:
由于这个图是可以跳转的,显然也是一个自动机,那么,如何构建这个自动机,就是我们接下来最大的问题。
在正式讲后缀自动机的构建前,我们要先讲几个基本概念
基本概念
定义
1.一个 SAM 必须要是一个 DAG,节点称作状态,边称作转移。
2.图存在一个源点叫初始状态,所有节点都可以从初始状态出发到达。
3.每个转移都代表了一个字母,从一个节点出发的转移互不相同。
4.存在若干个终止状态,从起点出发到这个终止状态的任一路径必定是原字符串的一个后缀,反之也应当成立。
5.在符合上面这四条的情况下,SAM 的节点数最少。
性质
与后缀 Trie 性质相同,此处不再赘述。
结束位置endpos
对于一个字符串"abcbc",那么它的子串bc在第 2,4 位置出现了,所以bc
有的情况下,有的子串的c
显然的,SAM 当中的每一个状态代表了以这个作为结束位置的子串,也就是
从这个
引理 1(充分性):字符串
的两个非空子串 的 相同时,当且仅当 在 中的出现是以 的后缀存在。
这个引理显然成立。
引理 2(必要性):两个非空子串
要么 ,要么 。
如果两个子串的
引理 3(连续性):将一个等价类当中的所有子串从小到大排序,那么前一个一定是后一个的后缀,且这些子串长度一定覆盖整个区间。
后缀链接link
我们考虑一个不是起始状态的状态
还有,这个字符串
所以,一个后缀链接
接下来,我们规定起始状态的 endpos:
引理 4:后缀链接构成一个以
为根的树。
由于后缀链接一定链接严格更短的字符串,所以构成一棵树。
引理 5:通过
集合构造的树(将子集和父集进行连边)与通过后缀链接构造的树相同。
在算法前:常用记号
算法
构建 SAM 的算法是一个在线的算法:我们依次加入字符串的字符,然后不断维护 SAM。
首先,起始的 SAM 只有一个状态
接下来,我们开始给当前字符串添加字符
1.我们先定义
2.我们创建一个新的状态
3.然后我们从状态
应用
回文树(回文自动机)**
类比(anal-o-gy):基于特定方面相似性对两个其他不同事物的比较。
——韦氏词典
待补。
Notes & References
附注
*:标*内容表示该内容为NOI 大纲中 NOI 级要求内容。
**:标**内容表示该内容NOI 大纲中不作要求。