字符串处理（上）

Andy Shen2023/8/25大约 25 分钟

前言

我们为什么要研究字符串问题？首先，因为字符串在生活当中十分常见：我们说的每一句话，每个单词，都是由一个或者多个字符串组合而成的。还有另外一个方面：字符串，是由字符组成的一个序列，研究字符串问题就是研究序列问题。

本篇文章分为上下两章：上章主要讲解哈希，Tries，Manacher，FA，KMP，BM 等基础内容，下章主要讲解 AC 自动机，后缀树，后缀自动机，回文自动机等进阶内容。

字符串哈希

弄糟（hash）：把...弄乱。

——韦氏词典

概念

何为哈希？我举一个例子：一个公司里面有很多人，这些人显然有自己的名字和姓氏（正确的废话）。那么在工作当中，我说“小张”“小刘”“小徐”，那么显然大家都能快速反应出这些人是谁。在这里，我们使用了人的姓氏来代表这个人本身，这就是一种摘要。哈希的本质就是将一个较长的信息，经过若干运算之后进行摘要（进行这若干运算的函数便是散列函数，又称哈希函数）。工业中常用的哈希算法有 MD5，SHA256 等。

接下来我们介绍一种非常简单的哈希，我们令一个哈希函数为 $H (x) = x * p_{1} \mod p_{2} (p_{1} \leq p_{2})$ ，其中 $p_{1}, p_{2}$ 为素数（下文 $p_{x}$ 均可认为是素数，除非特殊说明）。你可以自行举个例子，令 $p_{1} = 7, p_{2} = 13$ ，然后枚举 $x$ ，你可以发现对于相邻的 $x$ ，最后对应的 $H (x)$ 都会有很大的不同， $H (x)$ 的结果也都分布的比较均匀（事实上，这种算法和随机数的线性同余算法如出一辙，详见我的文章C++11 后更现代的数据生成）。这个小例子就能体现哈希在工业上一个很大的应用：当数据传输后，我可以对他进行哈希计算，如果数据传输过程中有微小的篡改，最后得到的哈希值会大大不同，那么文件发布者只要提供这个文件的哈希值，然后用户就可以通过哈希值比对来判断文件是否完整的传输到自己手里。

哈希表

我们对一个集合 $S_{1} = {x_{1}, x_{2}, x_{3}, \dots, x_{n}}$ 中的每个元素 $x$ 都进行散列函数操作得到一个新集合 $S_{2} = {H_{1}, H_{2}, H_{3}, \dots, H_{n}}$ 我们将 $H_{i}$ 作为下标， $x_{i}$ 作为元素存入一个数组当中，就可以得到一个哈希表。当我们需要查询一个元素是否在这个哈希表当中时，只要对这个元素进行散列运算得到的值作为下标，然后看这个下标有没有值即可。

Code

#include <bits/stdc++.h>

using namespace std;

constexpr int MAX_N = 10000;

inline int Hash(int x, int p1, int p2)
{
    return (x * p1) % p2;
}

int hmap[MAX_N];

int main()
{
    int n, q;
    cin >> n >> q;
    memset(hmap, 0xff, sizeof(hmap));
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        hmap[Hash(x, 7, 13)] = x;
    }
    for (int i = 1; i <= q; i++) {
        int x;
        cin >> x;
        if (hmap[Hash(x, 7, 13)] != -1) {
            cout << "YES" << endl;
        } else {
            cout << "NO" << endl;
        }
    }
    return 0;
}

哈希冲突

由于哈希是对元素的摘要，所以他势必会导致原数据的损失，例如开篇的那个例子当中，如果公司中有好几个姓李的，那么你叫小李就不知道是谁了。哈希也是一样，刚刚我们介绍的这种哈希，用鸽巢原理不难说明，当枚举超过 $p_{2}$ 个 $x$ 后，那么一定会出现两个 $x$ 的 $H (x)$ 是相同的。所以，衡量哈希函数的强度往往用冲突频率来衡量。

这种情况就叫做哈希冲突。遇到哈希冲突怎么办，一般有两种办法：1、凉办：啥都不干，冲突管他冲突，理论上只要我哈希函数的强度够大就不会冲突；2、我们将刚刚那段代码中的一维数组变为二维数组，然后对于有冲突的元素就放在第二维，然后对一个 $H (x)$ 我们一个个判断 $x$ 即可。

修改后的代码

#include <bits/stdc++.h>

using namespace std;

constexpr int MAX_N = 10000;
constexpr int CONFLICT = 10;

inline int Hash(int x, int p1, int p2)
{
    return (x * p1) % p2;
}

int hmap[MAX_N][CONFLICT];
int pos[MAX_N]; // 添加元素时判断当前位置

int main()
{
    int n, q;
    cin >> n >> q;
    memset(hmap, 0xff, sizeof(hmap));
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        int h = Hash(x, 7, 13);
        hmap[h][pos[h]++] = x;
    }
    for (int i = 1; i <= q; i++) {
        int x;
        cin >> x;
        int h = Hash(x, 7, 13);
        for (int i = 0; i < pos[h]; i++) {
            if (hmap[h][i] == x) {
                cout << "YES" << endl;
                break;
            }
        }
        cout << "NO" << endl;
    }
    return 0;
}

对序列的哈希

上面我们讲的这种哈希，是对单个元素进行计算，当这个问题被拓展到序列时，就不能这么干了。所以，接下来我们介绍一种常常用于字符串问题当中的哈希算法：BKDRHash（事实上，我研究过一下，这个算法和 Rabin-Karp 指纹算法本质上是一个东西）。

BKDRHash 的思路和刚刚的 Hash 是差不多的，但是由于序列的有序性，所以 BKDRHash 应该要有一种方式能够为不同的位提供一个不同的权重，从而使这个有序性得到保留。BKDRHash 的思路是将原字符串的每一位看成是一个 $p$ 进制数，然后我们将这个 $p$ 进制数转换成十进制数，并且模上一个大整数（通常这个数是 $2^{64} - 1$ ，也就是最大的 $u l l$ 数，这样子我们可以通过自然溢出来取模，避免低效的取模运算）。比如我们现在有一个字符串 $s = " a b a d c a d "$ ，我们令求解一个字符的 ASCII 值的函数为 $A (c)$ ，那么 BKDRHash 的散列函数 $H (x) = (A (s_{1}) * p_{1}^{6} + A (s_{2}) * p_{1}^{5} + A (s_{3}) * p_{1}^{4} + \dots + A (s_{7}) * p_{1}^{0}) \mod p_{2}$ ，这样，我们就将一个字符串转换为了一个值使得其能够被存储。

同时我们不得不注意到这个函数存在前缀性质。我们如果要求解这个串子串的哈希值（如求 substr[3,5]="adc"的哈希值），那么我们只要对这个字符串的全部前缀求一遍哈希，然后将两个前缀（"ab"，"abadc"）的哈希值相减得到的值 $^{'} a^{'} * p_{1}^{4} +^{'} d^{'} * p_{1}^{3} +^{'} c^{'} * p_{1}^{2}$ 除 $p_{1}^{2}$ 得到的结果（这里是模意义下，所以实际是要乘上 $p_{1}^{2}$ 关于 $p_{2}$ 的逆元），就是这个子串的哈希值。利用这个性质，我们就可以解决很多子串问题。

例题 1 字符串匹配（Rabin-Karp 算法）

字符串匹配，就是求解原文src中是否存在某个串pat。利用我们前述的前缀性质，我们对src的每个前缀进行哈希运算，然后对pat进行哈希运算。然后我们取src的每个子串，判断其哈希值是否与pat的哈希值相等，如果相等，那么就试做匹配上。

例题 2 最长回文串

我们要考虑到回文串有个神奇的性质：正读倒读都一样。所以我们对字符串正着的前缀做一遍哈希，反着的前缀做一遍哈希，然后枚举中心位置，二分长度，判断该子串正着读的哈希值和反着读的哈希值是否相同，若相同，则打擂答案，复杂度 $T (n) = O (n \log n)$

使用方法

通常来说，刚刚所述的 BKDRHash 只要 P=131 或者 13331，那么是很少遇到哈希冲突的，可以作为题目的一种标准解答看待。大部分子串问题，基本上可以如同例题 2 一样，枚举起始位置，二分长度，利用该函数的前缀性质计算出子串，然后对子串进行判断。

习题

1.不看给出的示例代码，自己实现一个哈希表，能够处理哈希冲突。

2.完成例题 2 的代码。

3.我们把形如"aaa","bb","cccc"的串叫做重串，请你写一段代码，判断出一个只包含小写字母的字符串（ $1 \leq | s | \leq 1 \times 10^{6}$ ）当中最长的重串。

Tries

字典（dic-tio-nary）：按字母顺序列出术语或名称的参考书。

——韦氏词典

Tries，又名字典树，这个名字正如 Treap 一样，是个合成词，由 Tree 和 Dictionaries 组合而成。字典树，顾名思义，可以像字典一样检索数据，又组织成了树形结构。事实上，字典树是一种前缀树：从根起到任一节点的路径边的所有权值组成的序列一定是一个或多个字符串的前缀。我放一幅图加深对这个前缀意义的理解。

我们将{'he','she','hers','his'}组织成字典树：

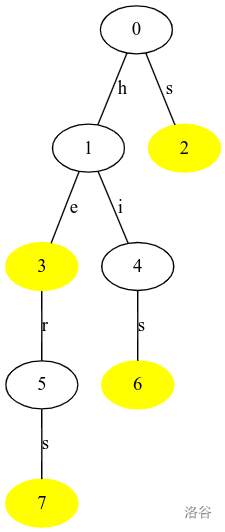
如图，黄色节点为终止节点。从 0 节点出发到这些终止节点的序列便是原来的字符串。

从本质上讲，字典树是对原来的所有串的一个压缩，我们将所有串相同前缀部分压缩到了同几个节点，从而使得它的性能更加优秀。

构建一颗 tries 的方法和构建一个链表差不多，一种是使用指针动态分配，还有一种是使用静态数组。我们依次读入字符串，然后将字符串插入 tries 中，如果没有对应节点分配一个节点，如果有了对应节点就跳转。

字典树很简单，但是字典树的前缀性质可以解决 LCP 问题（Longest Common Prefix）。字典树又将字符串问题转化成了图论问题，为之后的自动机算法打下了基础。

Code

模板题洛谷 P3879（这题要维护一下结束节点隶属于哪个文章）:

#include <bits/stdc++.h>

using namespace std;

constexpr int MAX_N = 200010;

int trie[MAX_N][26];
bool final[MAX_N];
set<int> nums[MAX_N];
int pos;

void insert(const string& str, const int num)
{
    int cur = 0;
    for (auto it : str) {
        if (trie[cur][it - 'a'] == 0) {
            trie[cur][it - 'a'] = ++pos;
        }
        cur = trie[cur][it - 'a'];
    }
    final[cur] = true;
    nums[cur].insert(num);
}

void check(const string& str)
{
    int cur = 0;
    for (auto it : str) {
        if (trie[cur][it - 'a'] == 0) {
            cout << endl;
            return;
        }
        cur = trie[cur][it - 'a'];
    }
    for (auto it : nums[cur]) {
        cout << it << ' ';
    }
    cout << endl;
}

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int l;
        cin >> l;
        for (int j = 1; j <= l; j++) {
            string str;
            cin >> str;
            insert(str, i);
        }
    }
    int m;
    cin >> m;
    for (int i = 1; i <= m; i++) {
        string str;
        cin >> str;
        check(str);
    }
    return 0;
}

#include <bits/stdc++.h>

using namespace std;

struct Node {
    Node* child[26] {};
    bool flag = false;
    Node()
    {
        memset(child, 0, sizeof(child));
    }
    set<int> nums;
};

Node* root = new Node;

void insert(const string& word, int num)
{
    Node* p = root;
    for (auto it : word) {
        if (p->child[it - 'a'] == nullptr) {
            p->child[it - 'a'] = new Node;
        }
        p = p->child[it - 'a'];
    }
    p->flag = true;
    p->nums.insert(num);
}

void check(const string& str)
{
    Node* p = root;
    for (auto it : str) {
        if (p->child[it - 'a'] == nullptr) {
            cout << endl;
            return;
        }
        p = p->child[it - 'a'];
    }
    for (auto it : p->nums) {
        cout << it << ' ';
    }
    cout << endl;
}

int main()
{
    int n;
    cin >> n;
    int l;
    for (int i = 1; i <= n; i++) {
        cin >> l;
        for (int j = 1; j <= l; j++) {
            string word;
            cin >> word;
            insert(word, i);
        }
    }
    int m;
    cin >> m;
    for (int i = 1; i <= m; i++) {
        string str;
        cin >> str;
        check(str);
    }
    return 0;
}

习题

洛谷 P3879 阅读理解

洛谷 P2922 Secret Message G（难度虚高）

洛谷 P4683 Type Printer（难度虚高）

Manacher 算法*

对称的（sym-met-ri-cal）：能被一平面分成两半。

——韦氏词典

Manacher 算法，又称“马拉车”算法（~~奇奇怪怪的谐音~~）。是一个可以在线性复杂度内求解回文串的算法。

首先，我们要知道什么叫回文串：存在一个对称轴，使得对称轴两边的字符串正好对称的字符串叫做回文串，比如 abccba 和 abcdcba。显然的，存在有一个性质，也就是回文串正读和反得到的结果相同。

在处理一个字符串的最长回文串前，我们先对字符串进行一番处理：对于形如abccba的字符串，它的对称轴并不是某一个具体的字符，与形如abcdcba的字符串不同。所以，我们在字符串的开头加上一个特殊符号~，结尾加个特殊符号!（注意，最开头的字母和最结尾的字母不应相同，不然算出来回文串值会大 1，这两个字符必须要加，从而在边界条件的时候仍然能计算出正确值），然后中间的所有字母之间都用#隔开（这里特殊字符的选用可以随意，只要是不常用到的不会出现在原串中的字符就行了）。那么上文所说的两个字符串将会分别变成~#a#b#c#c#b#a#!和~#a#b#c#d#c#b#a#!，同时，我们现在的新最长回文串的半径大小恰巧又等于原串的最长回文串大小。

接下来开始 Manacher 算法的核心部分：

我在江南讲动规的时候，经常讲一句话：考虑动态规划算法，你要考虑哪些地方存在复用？何为复用，就是如果当前计算结果和之前某个状态的计算结果相同时，我将之前计算出来的值直接用于本次计算，从而达到加速的效果。Manacher 算法的复用，恰恰是利用了回文串的回文性质。对于我们每次计算，维护两个值：之前计算出回文串最右端的值mr和计算出这个最右端时的中心值mid，利用这两个值我们也知道了这个最右端的值所对应的左端值ml。然后，我们将计算的结果放在p数组中。接下来，我们开始依次枚举中心点i。然后，如果i在区间 $[m i d, m r]$ 之间，由于回文串的回文性质，所以区间 $[m l, m i d]$ 的倒序串和 $[m i d, m r]$ 对应的串是完全相等的，这就意味着p[i]的值与p[mid*2-i]的值应该相等，此处就可以复用这个值；同时，要注意到， $p [i] + i - 1 \leq m r ⟺ p [i] \leq m r - i + 1$ ，也就是这个回文串不能超过右边界，最后的代码就是p[i] = min(p[mid * 2 - i], mr - i + 1);。如果i不在区间 $[m i d, m r]$ 之间，那么就无法复用，将p[i]置为 1 即可。接下来复用完了，开始暴力扩展回文串，然后更新mid,mr，最后打擂出答案即可。

Code

#include <bits/stdc++.h>

using namespace std;

constexpr int MAX_N = 22000010;

int p[MAX_N];
int mr, mid, ans;

int main()
{
    string iStr, str;
    cin >> iStr;
    str.push_back('~');
    str.push_back('~');
    str.push_back('#');
    for (auto it : iStr) {
        str.push_back(it);
        str.push_back('#');
    }
    str.push_back('!');
    // cout << str << endl;
    for (int i = 2; i < static_cast<int>(str.size()); i++) {
        if (i <= mr) {
            p[i] = min(p[mid * 2 - i], mr - i + 1);
        } else {
            p[i] = 1;
        }
        while (str[i - p[i]] == str[i + p[i]]) {
            ++p[i];
        }
        if (i + p[i] > mr) {
            mr = i + p[i] - 1;
            mid = i;
        }
        ans = max(ans, p[i]);
    }
    cout << ans - 1 << endl;
    return 0;
}

习题

（模板题）洛谷 P3805 manacher 算法

洛谷 P4555 最长双回文串

Manacher 的题目不多，上面这两个做了也就差不多了，其他的关于回文串的很多都是回文自动机的题目。

有限自动机（Finite Automation）*

自动机（au-tom-a-ton）：一种相对独立运行的机制。

——韦氏词典

正则表达式与 STL Regex

在讲自动机之前，不得不先讲一个东西叫做正则表达式(Regular Expression, Regex)。

什么是正则表达式？正则表达式是通过一定规则去匹配符合规则的字符串的过程。我举个例子：有十万个人的名字，我希望知道姓沈的人有多少，姓徐的人有多少，名字里带“亦”字的人有多少。这种问题就是正则表达式发挥神威的时候。对于刚刚这三个问题，我们可以分别通过规则"沈.*","徐.*",".*亦.*"，这里"."代表任意字符，"*"代表前面这个东西匹配任意次。这样我们就能够通过一系列规则去判断出很多东西（关于正则表达式具体规则，请自行学习参考资料）。

STL Regex

C++11 之后，C++加入了 Regex 库（NOI 的 C++标准是 C++14），正则表达式也就可以作为一个有效的工具来解决一系列字符串问题。

基本类型与构造函数

C++ Regex 的基本类型就是std::regex，这个类型代表了一条规则，它有好几个构造函数，不过最经常使用的构造函数还是explicit basic_regex( const CharT* s,flag_type f = std::regex_constants::ECMAScript );也就是使用一个字符串来构建匹配规则，同时允许指定语法规则。例如regex m1("aba.*");就新建了一个名为m1的匹配规则。

语法规则及其使用

C++的 regex 支持两种模式，一种是 ECMAScript 为首的 ECMA-262 文法（也是默认文法），还有一种是 POSIX 为首的 BRE 文法。这两种文法的主要区别在于，对于匹配规则".*(a|xayy)"和匹配串"zzxayyzz"，ECMA-262 是非贪婪的，它是找到一个符合条件的串即返回，在这个例子中，查询到"zzxa"就会返回；而 BRE 文法有最左最长的匹配规则：1.如果有多个长度不同串符合条件，那么就使用最长的那个；2.如果长度相等，选择最左，也就是最先找到的那个；在这个例子中，BRE 文法就会返回"zzxayy"。

如何指定语法规则？在调用构造函数的时候指定变量就行（如果同时需要几个语法规则，请使用|运算符隔开）。例如std::regex re2(".*(a|xayy)", std::regex::extended | std::regex::icase);就申明了一个忽略大小写拓展 POSIX 规则的语法规则。

指定语法规则有两部分：一部分是指定总的语法规则（ECMA or POSIX），还有一部分是指定小的语法规则（是否考虑大小写）。我将常用的列在下表中：

表一：

值	效果
icase	忽略大小写
optimize	加速匹配

表二：

值	效果
ECMAScript	使用 ECMAScript 规则
basic	使用基本 POSIX 文法
extended	使用拓展 POSIX 文法
awk	使用 awk 工具的 POSIX 文法
grep	使用 grep 工具的 POSIX 文法，等效于 basic+其他分隔符
egrep	使用 grep -E 的拓展 POSIX 文法，等效于 extended+其他分隔符

成员函数及其使用

前面讲的都是如何构造语法规则，接下来我们来讲如何使用。

一般常用的函数如下所示：

bool regex_match(string str, smatch& result, regex rules)：匹配一个正则表达式到整个字符序列。

bool regex_search(string str, smatch& result, regex rules)：匹配一个正则表达式到整个字符序列。

bool regex_replace()：以格式化的替换文本来替换正则表达式匹配的出现位置。

示例（来自 cppreference）

#include <iostream>
#include <iterator>
#include <string>
#include <regex>

int main()
{
    std::string s = "Some people, when confronted with a problem, think "
        "\"I know, I'll use regular expressions.\" "
        "Now they have two problems.";

    std::regex self_regex("REGULAR EXPRESSIONS",
            std::regex_constants::ECMAScript | std::regex_constants::icase); // 忽略大小写
    if (std::regex_search(s, self_regex)) {
        std::cout << "Text contains the phrase 'regular expressions'\n";
    }

    std::regex word_regex("(\\w+)");
    auto words_begin =
        std::sregex_iterator(s.begin(), s.end(), word_regex);
    auto words_end = std::sregex_iterator();

    std::cout << "Found "
              << std::distance(words_begin, words_end)
              << " words\n";

    const int N = 6;
    std::cout << "Words longer than " << N << " characters:\n";
    for (std::sregex_iterator i = words_begin; i != words_end; ++i) {
        std::smatch match = *i;
        std::string match_str = match.str();
        if (match_str.size() > N) {
            std::cout << "  " << match_str << '\n';
        }
    }

    std::regex long_word_regex("(\\w{7,})");
    std::string new_s = std::regex_replace(s, long_word_regex, "[$&]");
    std::cout << new_s << '\n';
}

自动机理论入门

这一节我将大概介绍自动机及其理论，关于其更加深入的内容，请参照《编译器设计》。

一个自动机是由一个五元组 $(Σ, Q, s, F, δ)$ ，其中， $Σ$ 表示字符集（也就是字符的取值范围）； $Q$ 表示状态集，相当于图的顶点； $s$ 表示起始状态； $F$ 表示接受状态，也可以看做截止状态，当读完串后处于接收状态那么这个自动机就接受这个字符串，反之就不接受这个字符串； $δ$ 表示转移函数，相当于图中的有向边。我们按照类似 Trie 的方式建图就能得到一个 FA。

如下图所示，展示了一个接受"a","ab","aac"的 FA。

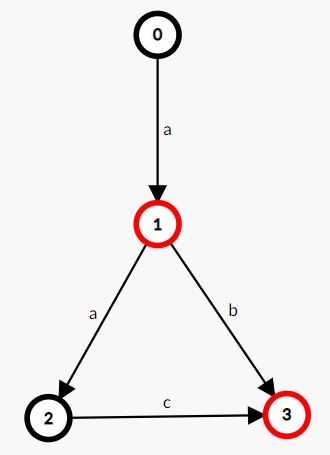
FA 我们一般可以当做一个有向图来看待，然后我们可以对一个串进行条件跳转，从而实现对字符串进行匹配的效果。

习题

洛谷 P7911 网络连接

这题有很多做法，可以尝试用 STL Regex，可以尝试用scanf的特殊输入方式（自行百度），可以尝试手写有限自动机，也可以写大模拟。

KMP 算法

匹配（match）：人或事相等或相似。

——韦氏词典

前缀函数

前缀函数 $π (i)$ 的定义是指对于一个字符串 $s$ 的前缀 $s [0. . . i]$ 的真前缀与真后缀最长匹配长度，例如"abab"的其中一个真前缀是"ab"，与其中一个真后缀"ab"相等，所以 $π (3) = 2$ 。要注意的是这里是指真前缀，也就是不包含原串的这种情况（显然的，如果包含原串的情况那么这个函数就不再具有它的意义）。

接下来我们可以考虑一下怎么求解这个前缀函数，显然的我们可以暴力：每次枚举原串的前缀长度，然后再枚举这个前缀的真前缀与真后缀的匹配长度 $j$ ，使用 substr 提取出这个真前缀和真后缀，然后比对是否相等，如相等打擂更新结果。这个方法显然是 $T (n) = O (n^{3})$ 的。

然后我们比较容易能够观察到其中一个优化：当我在尾部新加入一个字符时，这个字符要么和原真前缀的后面一个字符相等，要么不相等。如果相等，那么此时的 $π (i + 1) = π (i) + 1$ ；如果不相等，那就说明 $π (i + 1) < π (i) + 1$ ，那么我们枚举时真前缀和真后缀的匹配长度 $j$ 使得 $s [0. . j - 1] = s [i - j + 1 \dots i]$ 这一前缀性质仍然满足，此时我们只要判断第 $j$ 位和第 $i + 1$ 位是否相等，如果相等，我们就找到了 $π (i + 1)$ 的值是 $j$ （因为此时 $s [0 \dots j] = s [i - j + 1 \dots i + 1]$ ）如果不相等，就一直向下枚举直到 $j = 0$ 为止。此时由于我们从 $π (i)$ 往下枚举。所以大大降低了复杂度到 $T (n) = O (n^{2})$

接下来还有个不太显然的优化：我们先看一看刚刚这个算法的瓶颈在哪？瓶颈在于当不匹配时我们还是要枚举长度一个个进行字符串比较。那么我们能不能利用已经计算出来的前缀函数进行一般处理之后代替掉较慢的字符串匹配呢？这就是第二个优化的意义。

我举个例子：

\overset{π [i]}{\overset{⏞}{\underset{j}{\underset{⏟}{s_{0} s_{1}}} s_{2} s_{3}}} \dots \overset{π [i]}{\overset{⏞}{s i - 3 s i - 2 \underset{j}{\underset{⏟}{s i - 1 s i}}}} s_{i + 1}

当失配时，我们希望快速的找到一个数 $j$ 使得前缀性质仍然满足。观察刚刚这个图就能发现： $s [0. . j - 1] = s [i - j + 1 \dots i] = s [π (i) - j \dots π (i) - 1]$ （由于 $π (i)$ 的定义，所以真前缀等于真后缀，那么真前缀的长为 $j$ 的后缀也就等于真后缀长为 $j$ 的后缀，又由于 $j$ 满足前缀性质，所以 $j$ 长度的真前缀和 $j$ 长度的真后缀相等，结合一下，就能得到真前缀 $j$ 长度的前缀和真前缀 $j$ 长度的后缀相等）。仔细观察，不难发现，此时 $j$ 的长度与子串 $s [0 \dots π (i) - 1]$ 的前缀函数值等价。也就是 $j = π (π (i) - 1)$ 。所以， $j$ 从 $π (i) - 1$ 开始，到 $π (π (i) - 1) - 1$ 以此类推，所以我们可以得到 $j (n) = π (j (n - 1) - 1)$ ，从而得到如下图所示的代码：

vector<int> prefix_function(string s) {
    int n = (int)s.length();
    vector<int> pi(n);
    for (int i = 1; i < n; i++) {
        int j = pi[i - 1];
        while (j > 0 && s[i] != s[j]) j = pi[j - 1];
        if (s[i] == s[j]) j++;
        pi[i] = j;
    }
    return pi;
}

前缀，自动机，KMP

KMP 算法可以简单的被表述。假如原串为src，匹配串为pat，我们要求pat在src中出现的次数。那么我们组成一个新串s=pat++'#'++src，然后我们对这个新串求解前缀函数 $π (i)$ 。接下来我们读出每一个 $π (i)$ ，如果 $π (i) == | p a t |$ ，就说明此时 $s$ 的后缀（也就是此时src的后缀）与作为其前缀的pat相等，那就说明pat已经在src中完整出现了一次了，那么就可以统计答案。

vector<int> find_occurrences(string text, string pattern) {
    string cur = pattern + '#' + text;
    int sz1 = text.size(), sz2 = pattern.size();
    vector<int> v;
    vector<int> lps = prefix_function(cur);
    for (int i = sz2 + 1; i <= sz1 + sz2; i++) {
        if (lps[i] == sz2)
          v.push_back(i - 2 * sz2);
    }
    return v;
}

但是，这个 KMP 并不是我们常见的 KMP，因为这个 KMP 不光时间要消耗 $Θ (m + n)$ ，空间也要消耗 $Θ (m + n)$ 。

我们可以只对模式串pat求解它的前缀函数。然后我们使用它去匹配src，如果到某一位匹配不上了，此时，我们可以重复利用前面一段已经匹配的信息：由于前缀函数的性质，所以模式串前面这一段的前缀函数值就等于这一段的前缀和后缀最大相同部分，由于前缀后缀是相同的，所以此时我们将后缀作为新的前缀继续匹配。由于匹配指针是一直增加的，不回退的，所以 KMP 的复杂度是线性的。

同时，KMP 也可以被看做一个自动机，它的表达形式是这样：

δ (i, c) = {\begin{cases} i + 1 & s [i + 1] = c \\ 0 & s [1] \neq c \land i = 0 \\ δ (π (i), c) & s [i + 1] \neq c \land i > 0 \end{cases}

这个自动机也不难理解：当匹配上时，进入下一状态；当现在处于起始状态或者第一个字符就匹配不上时，就回归初始状态；如果只是单纯某一位匹配不上，那么此时我们要将后缀作为新的前缀继续开始匹配，此时这个自动机就应该退到 $π (i)$ 的状态。

对此更多内容，请详见Beta Shen - KMP 的“任督二脉”（KMP 字符串匹配导读）。

Boyer-Moore 算法**

优化（op-ti-mize）：使尽可能完美、有效或实用。

——韦氏词典

Boyer-Moore 是 KMP 的一种改进版，我此处并不想用很大的篇幅去介绍他，大概介绍一下两个规则和复杂度。

1.坏字符(Bad Character,BC)策略

众所周知，世界上不止英文字母，还有汉字集：假如我从一堆姓张的人里面找一个姓李的，那么肯定找不到。但是如果使用 KMP 的思路，你仍然要对原串进行一一匹配，这就会有大量无意义计算。接下来我们先考虑一种暴力的思路，我们统计每个字母是否在模式串当中出现。然后从右向左匹配，如果某一位匹配不上，判断这个字符有没有出现在模式串里过，如果没有，那么说明这个位置怎么都匹配不上，就直接跳过这个字符的位置。

但是光靠这个策略不够，我们还需要结合 KMP 的思路，也就是好后缀策略。

2.好后缀(Good Suffix,GS)策略

和 KMP 类似的，只不过我们是倒着求解这个前缀函数罢了。

通过上面这两个策略，最坏复杂度仍然保证了 $O (n + m)$ ，而最优复杂度优化到了 $Ω (n / m)$ ，这在字符集较大的时候是非常有利的。