前言

何为二叉搜索树（Binary Search Tree, BST）：二叉，说明了这棵树是棵二叉树；搜索，说明这棵树有搜索的功能。接下来我们通过一个实例来理解一下这里搜索的意思。

假如你有一个序列$\{1,4,2,3,5,6,8,11\}$，然后我要询问你一个问题：$8$和$12$是不是在这个序列当中。如果我们不考虑任何优化，那么暴力的做法就是一个个比对，直到比对上或者序列结束，复杂度$T(n)=O(n)$。当数据规模小的时候还能够接受，数据规模一大就显得有点太过复杂。当然了，有人会说可以用 STL 里面的set解决这个问题，如下列所示代码：

#include <bits/stdc++.h>

using namespace std;

set<int> seq;

int main()
{
    int n;
    cin >> n;
    while (n--) {
        int tmp;
        cin >> tmp;
        seq.insert(tmp);
    }
    int q;
    cin >> q;
    while (q--) {
        int tmp;
        cin >> tmp;
        if (seq.find(tmp) == seq.end()) {
            cout << "No" << endl;
        } else {
            cout << "Yes" << endl;
        }
    }
}

从实用主义的角度看，的确这样子问题就解决了，但是呢知其然更应知其所以然，set背后采用了红黑树这一数据结构，而红黑树正是二叉搜索树的一种。

从上面这个例子，大家应该就理解了二叉搜索树中搜索的意义，也就是对于区间进行查询。接下来我会在算法的具体解释中继续介绍一些其他二叉搜索树的性质。

本系列文章将分为上中下三个部分：上部会先从普通的 BST 开始，介绍 NOI 大纲中明确列出的四种 BST：AVL，Treap，笛卡尔树，Splay；中部将介绍一些比较常用但大纲中未列出的几种 BST：无旋 Treap（fhq Treap），替罪羊树，SBT，WBLT；下部将介绍一些比较复杂的 BST：2-3-4 树，红黑树，B 树，B+树。

普通的 BST

介绍

首先我们来想一想如何将数据从序列这种线性结构转换到树状结构。诸位应该都知道二叉树的中序排列吧，排列的顺序是左根右。假如我们构建一棵树，使得这棵树的中序排列是原序列从小到大排列过后的序列。那么当我们需要查找一个值的时候，比这个值小就向左子树，比这个值大就向右，如果匹配上就返回，如果遍历到叶子了还匹配不上就报错，就解决了这个问题。那么我们如何去构建这棵树呢？很简单，让左子树的所有节点小于根，右子树的所有节点都大于根。然后我们以第一个点为根，依次开始添加点，如果比当前的点小就放入左子树递归，如果比当前的点大就放入右子树递归，当递归到叶子节点的时候停止。接下来我们通过一个实例加深印象：

对于上面那个例子$\{1,4,2,3,5,6,8,11\}$，我先给出这些节点变成平衡树之后的图，然后再一步步模拟一番：

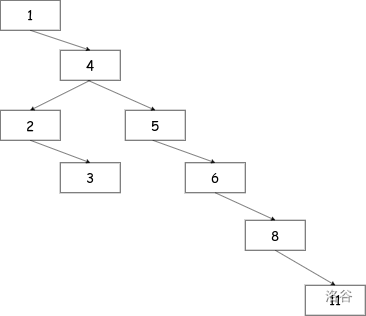
首先我们将 1 作为根，然后考虑 4，4 比 1 大，所以在 1 的右子树，此时 4 已经确定位置了，那么就放下；接下来我们考虑 2，2 比 1 大，所以在 1 的右子树，2 比 4 小，所以 2 在 4 的左子树，此时 2 位置确定；接下来我们考虑 3，3 比 1 大，在 1 的右子树，3 比 4 小，在 4 的左子树，3 比 2 大，在 2 的右子树，此时 3 位置确定；对于 5，6，8，11 以此类推，我不再赘述。

Code

按照刚刚这个思路，很容易就可以写出这种普通的 BST 的代码。接下来我给出 C++的代码，该代码我使用的是指针写法，其中put(char c, Node* cur)是将带有数据c的加到树上，而cur是用于递归的一个变量；get(char c, Node* cur)是查询c是否在树上，是则为true，否则为false，preorder(Node* cur)是递归输出中序遍历，结果应该是原序列排列后的结果。

// Primary Binary Search Tree
#include <bits/stdc++.h>

using namespace std;

struct Node {
    Node* l = nullptr;
    Node* r = nullptr;
    char lData = '\0';
    Node() = default;
    explicit Node(char c)
    {
        lData = c;
    };
};

Node root;

void put(char c, Node* cur)
{
    if (c >= cur->lData) {
        if (cur->r == nullptr) {
            Node* nNode = new Node;
            cur->r = nNode;
            cur->r->lData = c;
        } else {
            put(c, cur->r);
        }
    } else {
        if (cur->l == nullptr) {
            Node* nNode = new Node;
            cur->l = nNode;
            cur->l->lData = c;
        } else {
            put(c, cur->l);
        }
    }
}

bool get(char c, Node* cur)
{
    if (cur == nullptr) {
        return false;
    }
    if (cur->lData == c) {
        return true;
    } else if (c < cur->lData) {
        return get(c, cur->l);
    } else {
        return get(c, cur->r);
    }
    return false;
}

void preorder(Node* cur)
{
    if (cur == nullptr) {
        return;
    }
    cout << cur->lData;
    preorder(cur->l);
    preorder(cur->r);
}

int main()
{
    // freopen("data/bst1.in", "r", stdin);
    string str;
    cin >> str;
    root.lData = str.front();
    for (int i = 1; i < str.size(); i++) {
        put(str[i], &root);
    }
    preorder(&root);
    cout << endl;
    int n;
    char c;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> c;
        cout << get(c, &root) << endl;
    }
    return 0;
}

习题

基础题

1.请画出序列$\{5,2,7,3,1,4\}$对应的普通的 BST。

2.请画出序列$\{8,9,3,1,10,4\}$对应的普通的 BST。

3.请不看我给出的示例代码，自己写一遍 BST，要求：能够添加节点，能够查询节点，能够输出中序遍历。

思考题

4.如果给出的序列当中有重复的元素，应该怎么做。

5.如果我想要从刚刚那棵 BST 上删除一个节点，应该怎么做。

---

接下来我们接着上面的思路，介绍两种无修改的树：笛卡尔树，无修改的 Treap
如果我们给每个节点一个优先级，然后按照优先级进行重排后使用笛卡尔树的方式进行构建，就可以得到

笛卡尔树${}^1$

笛卡尔树是这样一种树：按照键值val它是一棵二叉堆（Heap），按照下标它是一棵二叉搜索树（Binary Search Tree），所以，笛卡尔树是一种特殊的 Treap，是 Tree 和 Heap 的合成词。我们分别考虑这两个性质：1.由于按照键值它是一棵堆，所以在根的那个值一定比左右子树的所有值都要小；2.又因为按照下标是个 BST，所以下标比较小的肯定在左子树，下标比较大的肯定在右子树。接下来我们就能够得到它的构建方式：根据性质 1，我们先选出序列当中最小的元素作为根，然后根据性质 2，我们将在该元素左边的所有元素作为左子树，该元素右边的所有元素作为右子树，然后分别递归处理即可得到我们要的笛卡尔树。

当然，在实践中并不会按照这个思路写，因为这个取出区间最小元素的操作并不是很方便（要用线段树或者 ST 表，但是这个开销并不小），所以实践当中是从左到右构造。从左到右构造是这样：我们维护一个单调栈，维护左右子树的最小节点；然后每次操作，我们考虑两种情况：1.当前处理节点i比前面的所有节点都要小，那么为了保证性质 1，i就应该作为根，又根据性质 2，最后一个出栈的节点（由于这是个单调栈，所以这个节点一定是前面节点当中最小的节点）就应该作为i的左子树；2.对于剩下的情况，说明i的大小刚刚好超过栈顶元素（单调栈的性质），为了维护性质 1，所以栈顶元素肯定要作为根，而又为了维护性质 2，所以要将原来的右子树作为i的左子树，将栈顶元素的右子树更新为子树i（这种情况下，考虑中序遍历，那么会先遍历原来的左子树，再遍历栈顶元素，再遍历原来的右子树，再遍历i，保证了性质 2）；然后操作完之后将元素入栈。

用途

这么一棵笛卡尔树是有一定用途的，由于性质 2，每棵子树的中序遍历将是原序列的一个子段，又由于性质 1，这棵子树的根将会是这个字段当中的最小值，所以，在笛卡尔树上两个节点之间的 LCA，将会是这两个位置中间所有元素在原序列当中的 RMQ。这个东西在 CSP2021-S 初赛的时候考过。

Code

洛谷笛卡尔树模板题：链接（这题卡常，要用快读）

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

ll a[10000000];

inline void qread(ll& ans)
{
    ans = 0;
    static char c = getchar();
    while (!isdigit(c))
        c = getchar();
    while (isdigit(c)) {
        ans = ans * 10 + c - '0';
        c = getchar();
    }
}

struct Node {
    ll l, r;
} tree[10000000];
ll n;

stack<ll> st;
ll root; //处理出根，用来遍历
inline void build()
{
    ll last = 1; //记录最后一个出队的节点
    st.push(1);
    for (int i = 2; i <= n; i++) {
        while (!st.empty() && a[i] < a[st.top()]) { //维护单调性
            last = st.top();
            st.pop();
        }
        if (st.empty()) {
            tree[i].l = last;
        } else {
            tree[i].l = tree[st.top()].r;
            tree[st.top()].r = i;
        }
        st.push(i);
    }
}

int main()
{
    qread(n);
    for (int i = 1; i <= n; i++) {
        qread(a[i]);
    }
    build();
    ll ans1 = 0, ans2 = 0;
    for (ll i = 1; i <= n; i++) {
        ans1 ^= i * (tree[i].l + 1);
        ans2 ^= i * (tree[i].r + 1);
    }
    cout << ans1 << ' ' << ans2 << endl;
    return 0;
}

习题

1.完成洛谷笛卡尔树模板题

2.尝试用笛卡尔树以及树链剖分 LCA完成 RMQ 问题的求解。

无修改的 Treap

方案是为了解决问题而生的，如果简单的 BST 就能够解决问题的话那么其它的 BST 是无意义的。事实上刚刚我们在手动模拟过程的时候就会发现，如果查询$11$这个节点就要进行 5 次判断，当我这个序列是单调增的时候，这棵二叉树就会变成一条链，也就是所谓的“退化”。理论上当二叉树是满的状态时，查询的速度应该是$T(n)=O(\log n)$的，但如果退化成链了，那么查询的速度就会下降至$T(n)=O(n)$，这个速度是远远不能接受的。为了解决退化的问题，不同的数据结构采取了不同的方案。当中无修改的 Treap 是理解起来最简单的一种（不涉及修改导致的旋转操作）。

我们再回头看一下退化成链的情况：那就是当序列单调增的时候会出现退化成链。那么只要改变这个序列结构就能够避免退化的情况，至于如何改变，便是随机化：我们用一个随机的数来替代刚刚笛卡尔树的下标，然后使用笛卡尔树的方法进行构建，就可以避免退化。

当然，事实上如果只是为了构建一棵树那么远远没有这么复杂，我只要将原序列随机排序一下，然后使用普通的方式依次插入序列即可。

---

上面那些都是无修改的树，这些树在实际应用当中其实用途并不是很大，接下来讲三种允许修改操作的树：AVL，Treap，Splay。

在介绍这些树之前，我要先讲一下旋转操作。

树的左旋和右旋

旋转操作是平衡操作的根本，分成两种基本操作：左旋(Left Rotate)和右旋(Right Rotate)。

我们先要考虑左旋右旋的目的，举一个简单的生活案例，你手上有一个纸带，怎么样让它变短？很简单，中间折一下就行。而左旋右旋就是类似这里“折一下的操作”，我们可以将一个链，以中间节点为新根折一下，然后得到一个新的子树，这个子树的深度比原来短且仍然符合中序遍历是排序序列这一性质。

接下来我们先介绍右旋操作。如下图所示，下图是一棵树的右旋。

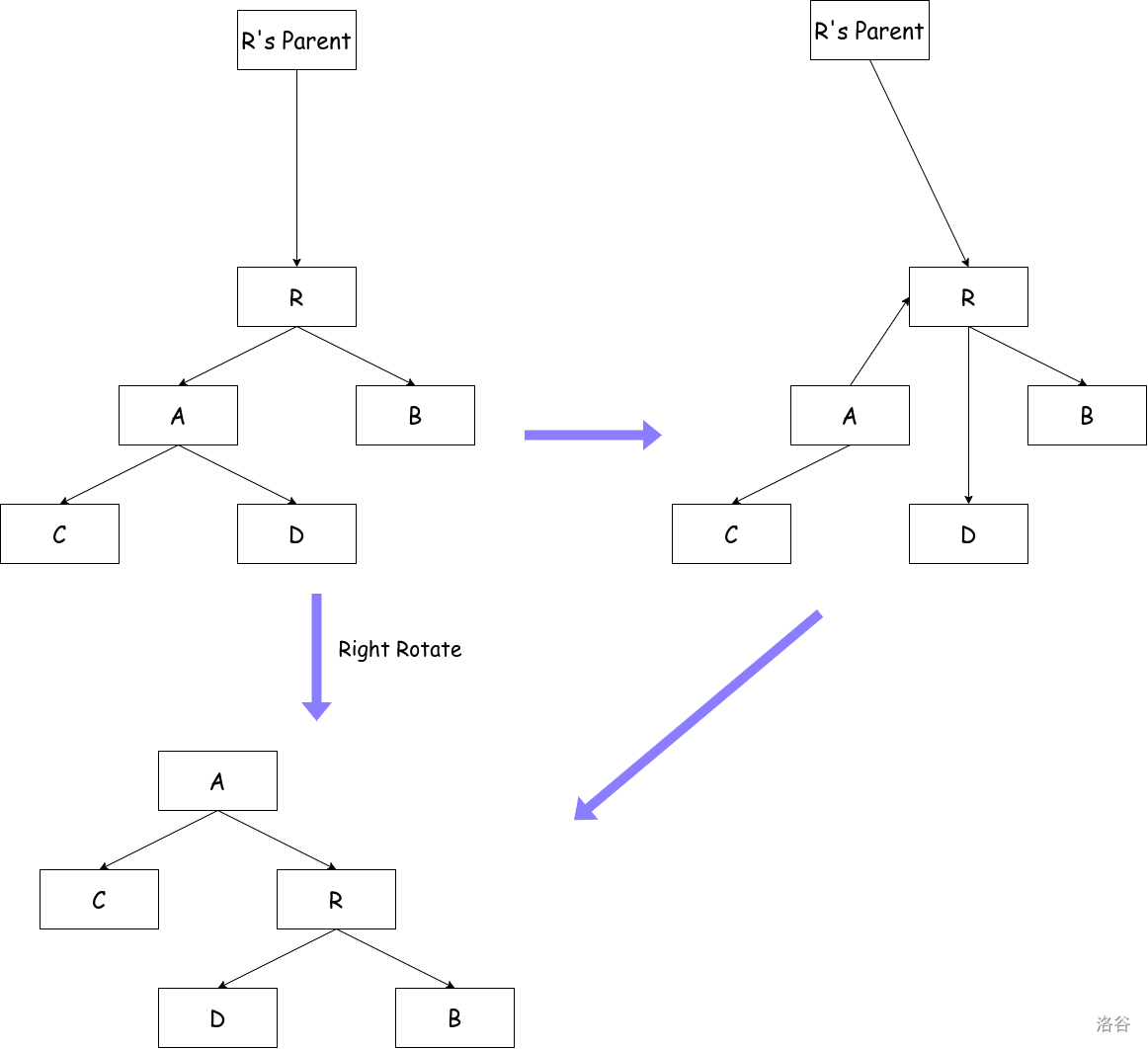
我们来模拟一下这个流程。首先伸出你的右手大拇指指向根$R$的左儿子$A$，然后握拳，像是将$R$和右子树拗过来一样，此时$C$所代表的左子树不变，而$R$和原来的右子树成为了新的右子树。但是因为这是一棵二叉树，此时有一个孤零零的$D$节点。我们根据 BST 的性质来判断它的性质：比 A 大，比 R 小，所以 D 应该在 R 的左子。此时就完成了一次以$R$为中心的右旋操作。

将这个过程写成伪代码如下（注意，旋转操作可以只针对一个子树，所以我们要同时维护原来 R 的父亲）：

right-rotate(r)
    tmp = r.left
    r.left = tmp.right
    tmp.right = r
    if r.par.left == r then
        r.par.left = tmp
    else
        r.par.right = tmp

类似的，我们可以推出左旋，左旋是右旋的逆过程，你将一棵树按根右旋一次再左旋一次就得到了原来的树，如下图所示：

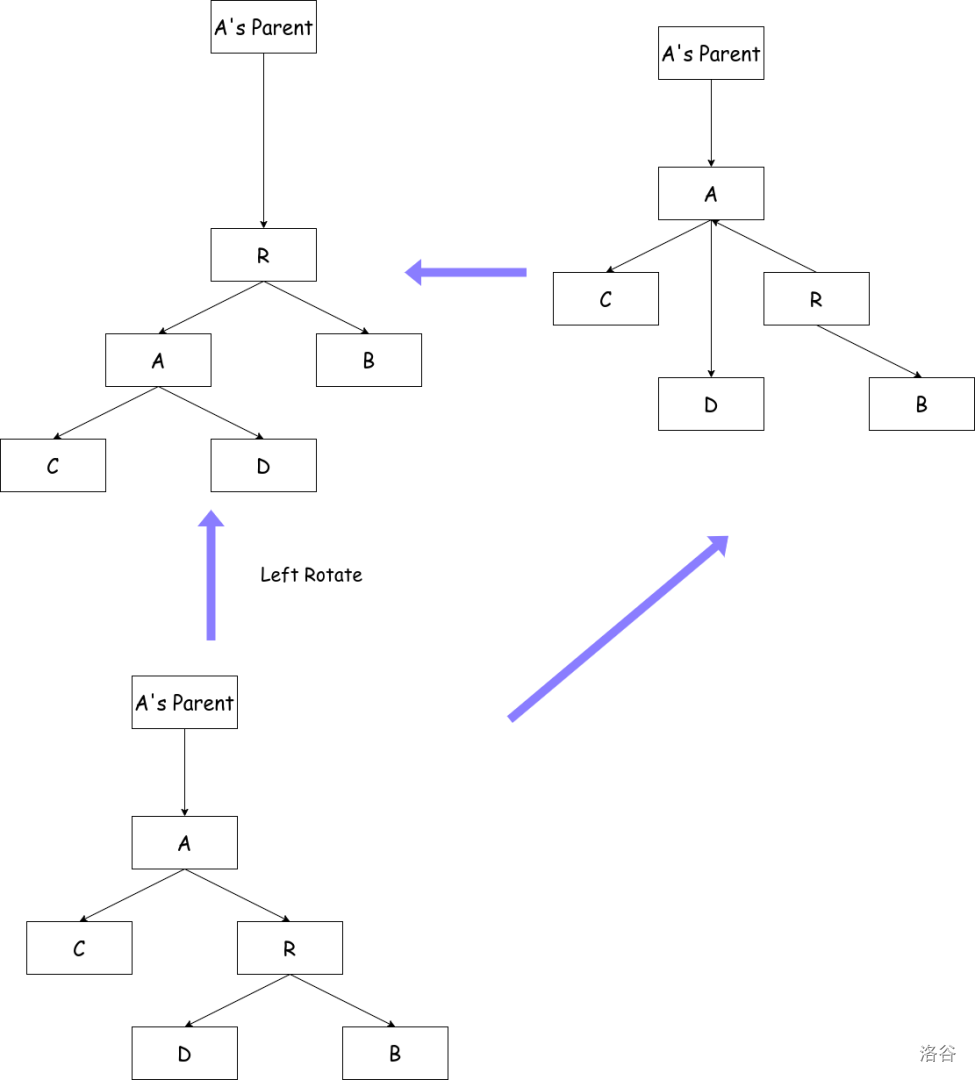
left-rotate(a)
    tmp = a.right
    a.right = tmp.left
    tmp.left = a
    if a.par.left == a then
        a.par.left = tmp
    else
        a.par.right = tmp

接下来我们可以观察一下左旋右旋的性质，从而为底下的用途做个铺垫。

仔细观察一下右旋操作（或者左旋操作），你会发现对根进行一次右旋操作后，得到的新树根左子树的深度会减小（因为新树的左子树是原来左子树的左子树，这话有点拗口，自行理解一下）。而新树的右子树的深度会变大（新树根的右子树的根是原来的根，从而使得高度变大）。

AVL 树

介绍

接下来，我先介绍一个最经典的 AVL 树。AVL 树的基本思路很简单，就是一旦不平衡就进行调整，调整的方式就是前面说的旋转操作。

首先，我们给出 AVL 树的一个递归定义${}^2$：

1.我们定义平衡因子$b(s)=h(l)-h(r)$，其中$h(x)$代表子树$x$的高度（自底向上的高度，又或者说是深度），$l,r$分别代表$s$的左右子树。

2.空二叉树是一棵 AVL。

3.一棵 AVL 树的左右子树也是 AVL 树，且对于树上任意非叶子节点$s$都存在$|b(s)|\le 1$。

4.树高为$O(\log n)$ ${}^3$

对于 AVL，它的插入，删除，查询的操作和前述的普通的 BST 并无差异，但是为了满足前述的性质 2，就需要有一个额外的操作，也就是平衡(balance)。

所以对于一棵 AVL 树，当平衡因子$b(r)=2$时，也就是左子树的深度比右子树的深度大 2 时，AVL 性质 2 被破坏，我们只要对$r$进行一次右旋操作，得到的新树的左子树深度和右子树深度差就会变小，从而维护了性质 2，这也就是平衡操作，当我们插入，删除后，考虑平衡因子不断进行维护，就可以得到一棵不错的二叉搜索树。

Code

由于 AVL 在 OI 实践当中用途不是很大，网上关于 AVL 的代码也足够多，我这里就不给出代码了。

Treap

待补

Splay

待补

Notes & References

1.这里对于笛卡尔树和 Treap 的定义是有歧义的，按照OI-Wiki上的讲法，认为 Treap 是一种特殊的笛卡尔树；而按照主流观点（洛谷以及 CCF 大纲），认为笛卡尔树是一种特殊的 Treap，此处我采用后面一种讲法。

2.此处递归定义的讲法参考自OI-Wiki上对于 AVL 的性质，但是从数理直觉的角度看，这个定义是一个递归定义（又或者说，是对Peano 公理在树上的一种类似推广），也是一种常用的定义手段。

3.这个性质是证明出来的而不是定义，对此的证明是通过解一个常系数非线性差分方程得到的，详情见OI-Wiki