算法复杂度分析

Andy Shen2022/8/30大约 11 分钟

如何表达算法复杂度

复杂度符号	定义	通俗理解
$Θ$ (Big theta)	渐进上下界	$=$
$O$ (Big O)	渐进上界	$\leq$
$Ω$ (Big Omega)	渐进下界	$\geq$
$o$ (Small o)	非紧上界	$<$
$ω$ (Small omega)	非紧下界	$>$

这是最严格的渐进符号，表示一个算法一定会执行的次数。此时，不存在什么最坏情况最好情况，举个例子，假如说我要使用暴力法来判断一个序列中有多少个数大于我给定的一个数，那么无论如何我都要比对 $n$ 次，那么这种情况下我可以使用 $Θ (n)$ 来表达这个东西的复杂度。但是再举个例子，如果我要找到一个序列中第一个大于我给定的数的数，那么我有可能需要比对 $n$ 次，但是更大可能是比对少于 $n$ 次，这种情况下，就不能使用 $Θ (n)$ 来表达这个东西的复杂度，而需要使用下方的 $O$ 来表示

$O$ (Big O)

这是相对宽松的一个渐进记号，表示一个算法最大会执行的次数，再以刚刚我举的那个例子为例，因为我比对次数最大是 $n$ 次，所以可以使用 $O (n)$ 来表达这个算法的复杂度。

由于在算法竞赛当中，我们要 AC 就要考虑所有数据的情况（包括最坏情况），所以我们看到用 $O$ 来表示的更多。

$Ω$ (Big Omega)

和 $O$ 一样， $Ω$ 给出的是下界，也就是最少会执行多少次，再以刚刚的的这个问题为例，因为最少可以比对 $1$ 次就解决问题，所以复杂度就是 $Ω (1)$

$o$ (Small o) & $ω$ (Small omega)

由于较少用到，如果有兴趣的请参见《算法导论》 $^{2}$ 第 29-30 页。

显然的，如果一个算法的上下界是一个相同数，或者说是 $O (g (n)) = Ω (g (n))$ （ $g (n)$ 是关于 $n$ 的一个函数，例如 $g (n) = n^{2}$ ，那么复杂度上界就是 $O (n^{2})$ ）

如何分析算法复杂度

经验法

经验法，就是靠 OI 选手多年做题的经验来判断一个算法的复杂度是多少。比如二分查找，由于每一次都是将问题折半，所以显然是 $T (n) = O (\log_{2} n)$ 的。那么下面我列一下常见算法的复杂度 $^{3}$ 。

1. $O (1)$

这就是所谓的常数复杂度，很多基本运算都是这个复杂度的，比如加减乘除等，注意，如果进行多次加减乘除，那么也视作是 $O (1)$ 的，只是这个常数大小不一样（常数大小不一样导致的问题可以看“如何看待算法复杂度”这一栏。所以知名的 $H a s h$ 算法基本上都视作是 $O (1)$ 的。

2. $O (\log_{2} n)$

对数的复杂度，这个复杂度是十分优秀的。二分查找，线段树（或者树状数组）的区间查询，二叉搜索树的查询以及添加节点等都是这个复杂度。在 $n$ 不是很大的时候，这个复杂度可以看做常数。（当然，卡卡也能卡掉）注意，常用 STL 中的 map 和 set 是使用红黑树实现的，插入，查询等复杂度均是 $O (\log_{2} n)$ ，而 C++11 新提出的 unordered_map 和 unordered_set 利用了 hash 算法，插入，查询等复杂度均是 $O (1)$ 的

注意，该复杂度比较常见的递归式是这样的：

T (n) = T (n / 2) + Θ (1)

T (1) = Θ (1)

3. $O (n)$

线性复杂度，在大部分情况下，这个复杂度仍然是优秀的，因为大部分问题中 $n$ 没那么大。出现这种复杂度，就说明有一重循环了（当然，循环内的操作仍然要是 $O (1)$ 的），常见线性表的查询等是这个复杂度。

注意，该复杂度比较常见的递归式是这样的：

T (n) = 2 T (n / 2) + Θ (1)

T (1) = Θ (1)

4. $O (n \log_{2} n)$

这个复杂度在排序算法当中比较常见，大部分先进的排序算法都是这个复杂度（当然不考虑桶排，计数排，基数排这些另类）。事实上，这个复杂度是在分治算法中更为常见，例如使用分治算法寻找最大字段和等。分治时，会将问题一分为二，阶数就会有 $\log_{2} n$ ，而每一层都是 $n$ 的复杂度，最后总复杂度就是 $O (n \log_{2} n)$ （具体为什么会有这种复杂度，看“递归树法”一栏即可）

注意，该复杂度比较常见的递归式是这样的：

T (n) = 2 T (n / 2) + Θ (n)

T (1) = Θ (1)

5. $O (n^{2})$

平方的复杂度，这个就说明出现了两重循环，而且这两重循环互不干涉（所以著名的欧拉筛也是两重，但是复杂度却是线性的，因为他第二重循环不会完全执行。）

6. $O (2^{n})$

爆搜的复杂度基本都是这个，某种意义上说，大部分爆搜的复杂度都是指数的，只是这个底不太一样，要注意，输出一个序列子集内容，也是这个复杂度（因为每个数都只有出现和不出现两种情况，所以总情况数就是若干个 2 相乘）

当然，还有 Floyd 算法的复杂度是 $O (n^{3})$ ，Edmonds-Karp 算法复杂度是 $O (V E^{2})$ ，Dinic，ISAP 算法的复杂度是 $O (V^{2} E)$ ，最高标号预流推进（HLPP）算法的复杂度是 $O (V^{2} \sqrt{E})$ 等，在做题过程中要注意积累，并且想一想他们为什么是这个复杂度。

递归树法

这才是这篇文章的重点，也是我真正想讲的东西。我们以一个例子为这一章节的开头。

T (n) = 2 T (n / 2) + Θ (1)

T (1) = Θ (1)

这是我们在 CSP 第一轮中很经常看到的一类题。很多人会讲，做这些题用主定理（主方法），但是我觉得对初学者教主定理是一种十分误人子弟的行为，因为主定理的证明十分复杂，而且不灵活，如果只是背下来主定理上考场，遇到复杂一点的题目就会直接崩溃。

我要讲的方法是递归树法，对于刚刚这个问题，我将这个递归方程从顶至底画出来，是这样的：

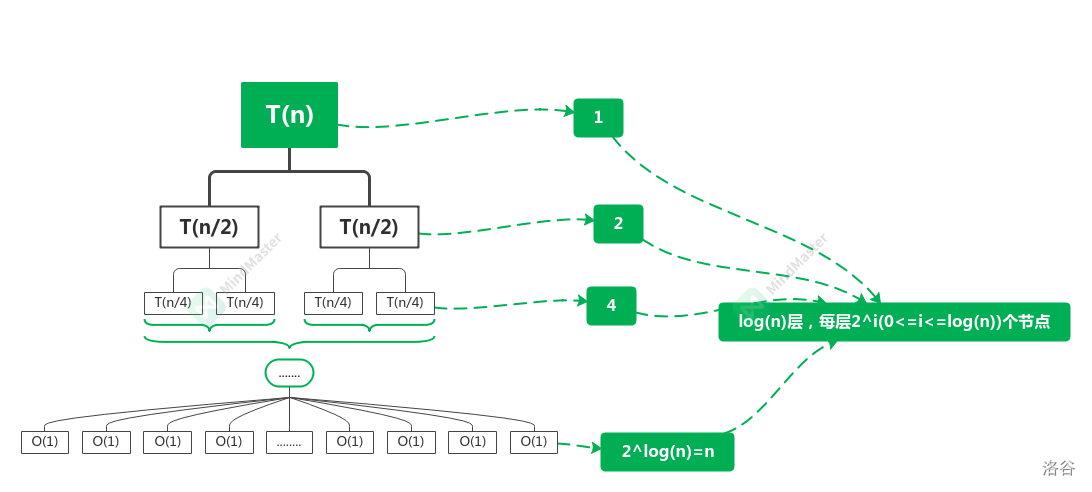
这个东西求和之后就能够得到 $T (n) = Θ (n)$ ，这就是递归树法，将时间复杂度的递归方程表达成树的形式，然后考虑每一层复杂度的加和，最后从上到下按层求和就能够得到复杂度的答案。

注：刚刚这个递归式其实就是线段树建树的递归式，线段树自底向上建树，从上到下看，每次将区间分成两段处理，每次只有一个操作（比如求最大值什么的），用刚刚的方法就可以算出来他是线性的。

刚刚的递归树法的应用还有很多，但是无论如何，这种思想，也就是将情况画成树的思想，是最重要的。

主定理

主定理就是人家总结好的一个经验主义的公式，只要知道内容本身即可，而证明过程过于复杂，我此处不列，有兴趣的自行查看《算法导论》第 55-58 页。

主定理给形如

T (n) = a T (n / b) + f (n)

的式子提供了一种“菜谱式”的解决方法

主定理 $^{4}$ $^{5}$ ：

对于两个函数 $n^{\log_{b} a}$ 和 $f (n)$ ：

1、如果 $n^{\log_{b} a}$ 更大（注意，此时更大的意思是当 $n$ 取到一个极大值时，两个函数中这个更大），那么复杂度 $T (n) = Θ (n^{\log_{b} a})$

2、如果 $f (n) = n^{\log_{b} a}$ ，那么复杂度 $T (n) = Θ (n^{\log_{b} a} \log n)$

3、如果 $f (n)$ 最大，那么复杂度 $T (n) = Θ (f (n))$

可以自己试一试用主定理解决刚刚那个问题，当然，我还是推荐使用更为通用的递归树法。

主定理的局限性：

我此处给出的主定理是没有附加条件的，的确，这个形式用起来非常方便，但是如果看过《算法导论》，就会发现主定理其实是有一些附加条件的。例如，对于形如（这个地方有待考证）：

T (n) = a T (n / b) + n \log n

的形式，那么这种情况下，主定理就无法使用（所谓的落入了情况 2 和情况 3 之间的“空隙”）

如何看待算法复杂度

我先给大家看一张关于运行时间的表格 $^{6}$ ，当我们估计出算法复杂度后，将值带入算法复杂度的式子中，计算一下执行次数（例如复杂度 $O (n^{2})$ ，如果 $1 \leq n \leq 1000$ ，那么执行次数大约就是 1000000），然后用下表就可以判断你这个代码是否能 AC。

执行次数	可行性
1000000	游刃有余
10000000	勉勉强强
100000000	很悬，仅限循环体非常简单的情况

上面这个表格十分有用，有的时候，可以通过数据来判断应该设计多大复杂度的一个算法。

算法复杂度还是要理性看待的，举个例子，网络流中的 Dinic 算法，复杂度是 $O (V^{2} E)$ ，但是事实上，在随机图上，这玩意跑的巨快，基本上一千多个点，几万条边他仍然能够在时限内跑完的。还有著名（~~人人喊打~~）的 SPFA 算法在随机图中表现的也十分好，但是他实际复杂度还是 $O (n m)$ 的（所以个人很反对有人直接给他复杂度标成 $O (k n)$ 的做法，因为这是不符合 $O$ 这个渐进记号的定义的。所以可能 $Ω (k n)$ 的这种表达方式是更为正确的）。这两类都是在随机数据上可以跑出很好成绩的。而另外还有一类，比如块状链表在解决第 k 大问题中，也表现的和 BST 差不多，尽管它复杂度大，但奈何不住它常数小啊。所以判断一个算法能不能跑过，要分两步：

1、理论分析

首先看算法复杂度和执行次数，用我刚刚那个表格比对一下；然后看常数大小，尽可能避免使用乘除（因为乘除要百来个时间周期，加减移位等只要几十个甚至十来个）使常数尽可能小；最后看这个算法能够有多少复用（就是能否避掉大量重复计算，例如 Dinic 中的当前弧优化炸点优化等，这个就能判断出随机数据过不过的去）

2、实际分析

多造数据多测试，造一些符合数据范围的随机大数据，这样子可以避免很多 TLE 的问题（当然，出题人故意卡你，那就自求多福吧）。

另外，如果你设计了一个超出了标程复杂度的一个算法（最经典的就是 $O (n)$ 和 $O (n \log n)$ ），如果你有能力的话，建议不要使用 STL 以及一些 C++高级特性，在有些地方卡卡常，有不小的希望能过。（毕竟在 $n \leq 1 e 6$ 的情况下， $\log n$ 也就不过是十几的样子，要是有的地方的速度能达到原来的常数倍，那么也许就过了）

引用

[1]：https://blog.csdn.net/so_geili/article/details/53353593

[2]:《Introduction to Algorithms(Third Edition)》（中译名《算法导论（第三版）》Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 著，殷建平，徐云，王刚，刘晓光，苏明，邹恒明，王宏志译，机械工业出版社出版，以下《算法导论》均指该书）

[3]：《算法竞赛入门到进阶》（罗永军，郭卫斌著，清华大学出版社出版）

[4]：《算法导论》第 53-54 页

[5]：https://zhuanlan.zhihu.com/p/113406812

[6]：《挑战程序设计竞赛（第二版）》（【日】秋叶拓哉，岩田阳一，北川宜稔著，巫泽俊，庄俊元，李津羽译，陈越，翁凯，王灿审，机械工业出版社出版）